Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол OVT. Ответ дайте в градусах.
SO=VO (т.к. это радиусы окружности)
SO=VO=ST=TV (по
определению ромба)
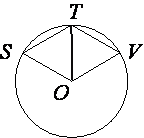Проведем отрезок OT.
OT тоже радиус окружности, следовательно OT=SO=VO=ST=TV
Следовательно, треугольники STO и TVO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
Следовательно и ∠OVT=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
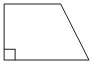Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Какое наибольшее число коробок в форме прямоугольного параллелепипеда размером 30Х40Х50 (см) можно поместить в кузов машины размером 3Х2Х3,5 (м)?
Какие из следующих утверждений верны?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: