Сторона ромба равна 8, а расстояние от центра ромба до неё равно 2. Найдите площадь ромба.
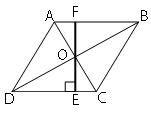Обозначим ключевые точки как показано на рисунке.
Проведем продолжение высоты OE к стороне AB и обозначим точку пересечения как F (как показано на рисунке).
Площадь
ромба (как и
параллелограмма) равна произведению высоты на сторону ромба.
Высота ромба = EF (т.к. EF перпендикулярна CD). Рассмотрим треугольники DOE и BOF.
DO=OB (по второму
свойству ромба)
∠DOE=∠BOF (т.к. они
вертикальные)
∠EDO=∠FBO (т.к. это
внутренние накрест-лежащие)
Следовательно, треугольники DOE и BOF равны по
второму признаку.
Тогда OE=OF => EF=2*OE=2*2=4
Sромба=EF*CD=4*8=32
Ответ: Sромба=32
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) У равнобедренного треугольника есть ось симметрии.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
Катеты прямоугольного треугольника равны 3√
Прямые m и n параллельны. Найдите ∠3, если ∠1=22°, ∠2=72°. Ответ дайте в градусах.
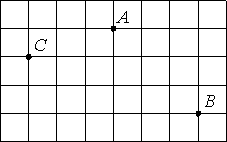На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2020-04-07 20:57:31) XXX_TNT_XXX: сторона ромба 20 см а острый угол равен 60 найдите длину меньшей диагонали
(2014-05-12 19:49:56) Администратор: Валерия, да, площадь ромба можно вычислить и через половину произведения диагоналей, но в этой задаче удобней через сторону и высоту.
(2014-05-12 17:55:12) Валерия : Разве площадь ромба не половина произведения его диагоналей?