
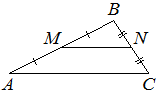
 Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.
MN -
средняя треугольника по определению.
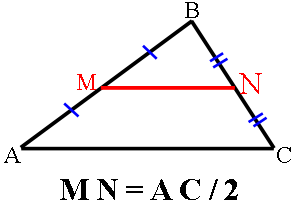
Тогда, по теореме о средней линии:
MN=AC/2=34/2=17
Ответ: 17
Поделитесь решением
Присоединяйтесь к нам...
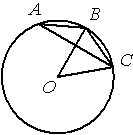 Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
 На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
 Катеты прямоугольного треугольника равны 8 и 6. Найдите синус наименьшего угла этого треугольника.
Катеты прямоугольного треугольника равны 8 и 6. Найдите синус наименьшего угла этого треугольника.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=17. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=17. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Комментарии: