
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ673 –ł–∑ 1087 |
 –í —ā—Ä–į–Ņ–Ķ—Ü–ł—é, —Ā—É–ľ–ľ–į –ī–Ľ–ł–Ĺ –Ī–ĺ–ļ–ĺ–≤—č—Ö —Ā—ā–ĺ—Ä–ĺ–Ĺ –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —Ä–į–≤–Ĺ–į 18, –≤–Ņ–ł—Ā–į–Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É —Ā—Ä–Ķ–ī–Ĺ–Ķ–Ļ –Ľ–ł–Ĺ–ł–ł —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
–í —ā—Ä–į–Ņ–Ķ—Ü–ł—é, —Ā—É–ľ–ľ–į –ī–Ľ–ł–Ĺ –Ī–ĺ–ļ–ĺ–≤—č—Ö —Ā—ā–ĺ—Ä–ĺ–Ĺ –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —Ä–į–≤–Ĺ–į 18, –≤–Ņ–ł—Ā–į–Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É —Ā—Ä–Ķ–ī–Ĺ–Ķ–Ļ –Ľ–ł–Ĺ–ł–ł —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
–ü–ĺ –≤—ā–ĺ—Ä–ĺ–ľ—É —Ā–≤–ĺ–Ļ—Ā—ā–≤—É —á–Ķ—ā—č—Ä–Ķ—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į:
AB+CD=BC+AD=18
–ü–ĺ
–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é —Ā—Ä–Ķ–ī–Ĺ–Ķ–Ļ –Ľ–ł–Ĺ–ł–ł —ā—Ä–į–Ņ–Ķ—Ü–ł–ł: m=(BC+AD)/2=18/2=9
–ě—ā–≤–Ķ—ā: m=9
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–į –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į AL, —É–≥–ĺ–Ľ ALC —Ä–į–≤–Ķ–Ĺ 52¬į, —É–≥–ĺ–Ľ ABC —Ä–į–≤–Ķ–Ĺ 13¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ACB. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–į –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į AL, —É–≥–ĺ–Ľ ALC —Ä–į–≤–Ķ–Ĺ 52¬į, —É–≥–ĺ–Ľ ABC —Ä–į–≤–Ķ–Ĺ 13¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ACB. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
 –¶–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ—č–Ļ —É–≥–ĺ–Ľ
AOB —Ä–į–≤–Ķ–Ĺ 60¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É —Ö–ĺ—Ä–ī—č AB, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä—É—é –ĺ–Ĺ –ĺ–Ņ–ł—Ä–į–Ķ—ā—Ā—Ź, –Ķ—Ā–Ľ–ł —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ 5.
–¶–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ—č–Ļ —É–≥–ĺ–Ľ
AOB —Ä–į–≤–Ķ–Ĺ 60¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É —Ö–ĺ—Ä–ī—č AB, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä—É—é –ĺ–Ĺ –ĺ–Ņ–ł—Ä–į–Ķ—ā—Ā—Ź, –Ķ—Ā–Ľ–ł —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ 5.
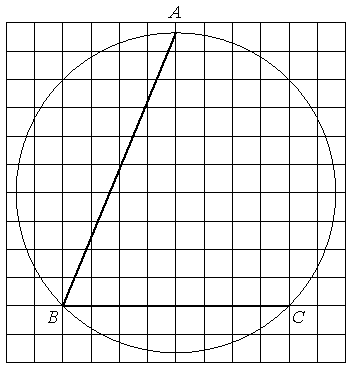 –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ABC. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ABC. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
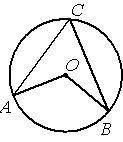 –Ę–ĺ—á–ļ–į –ě ‚Äď —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, /ACB=70¬į (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į AOB (–≤ –≥—Ä–į–ī—É—Ā–į—Ö).
–Ę–ĺ—á–ļ–į –ě ‚Äď —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, /ACB=70¬į (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į AOB (–≤ –≥—Ä–į–ī—É—Ā–į—Ö).
 –•–ĺ—Ä–ī—č AC –ł BD –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ P, BP=12, CP=15, DP=25. –Ě–į–Ļ–ī–ł—ā–Ķ AP.
–•–ĺ—Ä–ī—č AC –ł BD –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ P, BP=12, CP=15, DP=25. –Ě–į–Ļ–ī–ł—ā–Ķ AP.

 , –ł–Ľ–ł
, –ł–Ľ–ł  , –≥–ī–Ķ m - —Ā—Ä–Ķ–ī–Ĺ—Ź—Ź –Ľ–ł–Ĺ–ł—Ź —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
, –≥–ī–Ķ m - —Ā—Ä–Ķ–ī–Ĺ—Ź—Ź –Ľ–ł–Ĺ–ł—Ź —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: