Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Рассмотрим
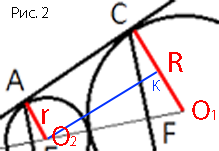
трапецию ACO1O2
Данная трапеция
прямоугольная, т.к. радиусы перпендикулярны
касательной AC (по
свойству касательной).
Проведем O2K параллельно AC, O2K=AC, т.к. ACKO2 -
прямоугольник.
По
теореме Пифагора:
(O1O2)2=(O2K)2+(KO1)2
(R+r)2=(O2K)2+(R-r)2
(100+25)2=(O2K)2+(100-25)2
15625=(O2K)2+5625
(O2K)2=10000
O2K=100=AC
Рассмотрим треугольники OAO2 и OCO1 (cм. Рис.1).
∠AOO2 - общий
∠OAO2=∠OCO1=90°
Следовательно эти треугольники
подобны (по
первому признаку подобия треугольников).
Тогда, R/r=OC/OA
100/25=OC/AO=(AO+AC)/AO
4AO=AO+100
3OA=100
OA=100/3
Из
подобия этих же треугольников:
R/r=O10/O2O
R/r=(O2O+R+r)/O2O
100/25=(O2O+100+25)/O2O
4(O2O)=O2O+125
3(O2O)=125
O2O=125/3
Обозначим угол ∠AOO2 как α
cosα=OA/OO2=(100/3)/(125/3)=100/125=0,8
Посмотрим на треугольники OAE и OCF.
Они
прямоугольные по
второму свойству хорды.
Тогда для треугольника OAE:
cosα=OE/OA
OE=OA*cosα=(100/3)*0,8=80/3
Для треугольника OCF:
cosα=OF/OC
OF=OC*cosα=(OA+AC)*cosα=
(100/3+100)*0,8=80/3+80=(80+3*80)/3=320/3
EF=OF-OE=320/3-80/3=240/3=80
Ответ: EF=80
Поделитесь решением
Присоединяйтесь к нам...
Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=42. Найдите MN.
ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 136. Найдите стороны треугольника ABC.
Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80. Найдите расстояние от хорды AB до параллельной ей касательной k.
Укажите номера верных утверждений.
1) Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая медиана равнобедренного треугольника является его биссектрисой.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: