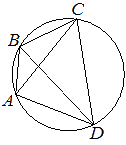Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
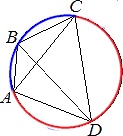∠ABC является вписанным углом и опирается на дугу ADC (красная).
Следовательно, по теореме о вписанном угле, градусная мера дуги ADC равна 138°*2=276°
Тогда градусная мера синей дуги равна 360°-276°=84°
∠ADC тоже является вписанным углом и опирается на дугу ABC (синяя).
Следовательно, по той же теореме о вписанном угле∠ADC=84°/2=42°.
Рассмотрим треугольник ACD.
По теореме о сумме углов треугольника запишем:
180°=∠ADC+∠CAD+∠ACD
180°=42°+83°+∠ACD
180°-42°-83°=∠ACD
∠ACD=55°
Заметим, что углы ACD и ABD являются вписанными и опираются на одну и ту же дугу.
Следовательно, эти углы равны, ∠ACD=∠ABD=55°
Ответ: 55
Поделитесь решением
Присоединяйтесь к нам...
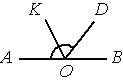Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=52°. Ответ дайте в градусах.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
В трапеции ABCD AD=3, BC=1, а её площадь равна 12. Найдите площадь треугольника ABC.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
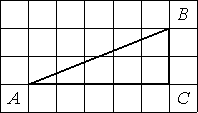Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: