
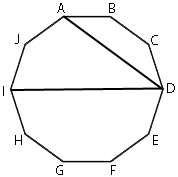
 ABCDEFGHIJ – правильный десятиугольник. Найдите угол ADI. Ответ дайте в градусах.
ABCDEFGHIJ – правильный десятиугольник. Найдите угол ADI. Ответ дайте в градусах.
Вариант 1 (Предложил пользователь Светлана)
 Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
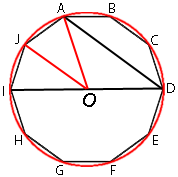
Очевидно, что отрезки, проведенные из центра окружности к углам девятиугольника образуют равные углы, так как разбивают девятиугольник на равные треугольники.
Такой угол (например ∠AOJ) равен 360°/10=36°
Тогда ∠AOI равен:
∠AOI=36°*2=72°
∠AOI является
центральным, следовательно градусная мера дуги IJA тоже равна 76°
∠ADI тоже опирается на эту же дугу, но является
вписанным, следовательно:
∠ADI=72°/2=36° (по
теореме о вписанном угле)
Ответ: 36
 Проведем отрезки AC и BD.
Проведем отрезки AC и BD.Поделитесь решением
Присоединяйтесь к нам...
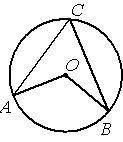 Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
 Сторона ромба равна 24, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 24, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
 Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, описанной около этого треугольника.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, описанной около этого треугольника.
Комментарии: