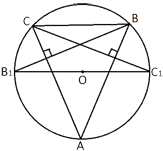
Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
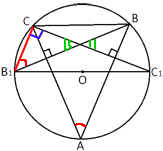∠BAC является
вписанным углом и опирается на малую дугу CB.
Проведем отрезок CB1, ∠CB1B тоже является
вписанным и опирается на ту же дугу, следовательно, ∠BAC=∠CB1B.
B1C1 является диаметром окружности, так как проходит через ее центр. Следовательно, B1C1 делит окружность на две дуги по 180°
∠B1CC1 тоже
вписанный и опирается на дугу в 180°, по
теореме о вписанном угле ∠B1CC1=180°/2=90°.
Обозначим еще три точки, как показано на рисунке ниже:
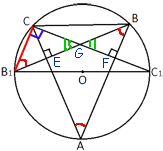Точки E и F - точки пересечения
высот и сторон треугольника ABC, G - точка пересечения
высот.
Рассмотрим треугольники B1CG и BFG.
∠CGB1=∠BGF (так как они
вертикальные).
∠B1CG=∠BFG (так как они оба прямые).
Следовательно, по
теореме о сумме углов треугольника, ∠СB1G=∠GBF
Следовательно, ∠GBF так же равен и ∠BAC
Рассмотрим треугольник AEB.
∠AEB=90° (так как BE -
высота).
∠BAC=∠GBF
Тогда, используя
теорему о сумме углов треугольника получаем, что каждый из углов BAC и GBF равен по 45°.
Ответ: ∠BAC=45°
Поделитесь решением
Присоединяйтесь к нам...
На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
Площадь круга равна 90. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 72°. Найдите величину угла OMK. Ответ дайте в градусах.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
140°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: