Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
Проведем отрезок CO.
Рассмотрим треугольник ACO.
∠ACO=∠ACB/2=28°/2=14° (по
второму свойству касательной).
∠CAO=90° (по
первому свойству касательной)
По
теореме о сумме углов треугольника:
180°=∠AOC+∠ACO+∠CAO
180°=∠AOC+14°+90°
∠AOC=76°
Рассмотрим треугольники ACO и BCO.
OC - общая сторона
AC=BC (по
второму свойству касательной)
OA=OB (т.к. это радиусы)
Следовательно, по
третьему признаку, данные треугольники равны.
Тогда и ∠AOC=∠BOC=76°
Рассмотрим треугольник AOB.
OA=OB (т.к. это радиусы)
Следовательно, треугольник AOB -
равнобедренный.
Тогда ∠BAO=∠ABO (по
свойству равнобедренного треугольника).
По
теореме о сумме углов треугольника:
180°=∠AOB+∠OAB+∠ABO
180°=∠AOC+∠BOC+2∠ABO
180°=76°+76°+2∠ABO
28°=2∠ABO
∠ABO=14°
Ответ: 14
Поделитесь решением
Присоединяйтесь к нам...
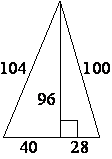Найдите площадь треугольника, изображённого на рисунке.
Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 36.
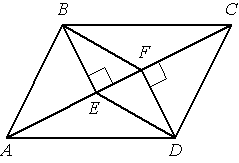В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
В трапеции ABCD основания AD и BC равны соответственно 34 и 9, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=10.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: