
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=17. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=17. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Рассмотрим треугольники ADC и CBD.
 ∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается
вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по
теореме).
∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается
вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по
теореме).
∠CDB - общий для обоих треугольников, следовательно, по
признаку подобия, треугольники ADC и CBD -
подобны.
Следовательно, по определению подобных треугольников запишем:
CD/BD=AC/BC=AD/CD
AC/BC=AM/MB=7/17 (по первому
свойству биссектрисы).
Получаем, что:
AD/CD=7/17
AD=CD*7/17
И...
CD/BD=7/17
17CD=7BD
BD=CD*17/7
BD=AD+AB=AD+17+7=AD+24
AD+24=CD*17/7
Подставляем значение AD, которое получили ранее AD=CD*7/17
CD*7/17+24=CD*17/7
24=CD*17/7-CD*7/17
Приводим к общему знаменателю:
24=(17*17*CD-7*7*CD)/(17*7)
24=(289CD-49CD)/119
24*119=289CD-49CD
24*119=240CD
CD=24*119/240=119/10=11,9
Ответ: CD=11,9
Поделитесь решением
Присоединяйтесь к нам...
 Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
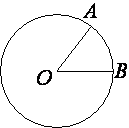 На окружности с центром O отмечены точки A и B так, что
/AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
На окружности с центром O отмечены точки A и B так, что
/AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
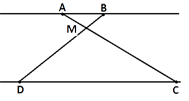 Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=15, DC=30, AC=39.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=15, DC=30, AC=39.
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
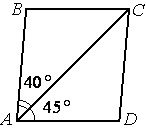 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол параллелограмма.


Комментарии: