
 На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
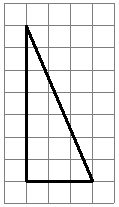
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Из
определения прямоугольного треугольника понятно, что катеты - это стороны прилегающие к прямому углу. В данной задаче катеты равны 7 и 3.
Очевидно, что 7 - длина большего катета.
Ответ: 7
Поделитесь решением
Присоединяйтесь к нам...
 Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
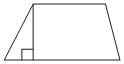
Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 163°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 163°. Найдите угол C. Ответ дайте в градусах.
 Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=7, DK=14, BC=10. Найдите AD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=7, DK=14, BC=10. Найдите AD.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=17. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=17. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.

Комментарии: