
Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Рассмотрим каждое утверждение:
1) "Площадь
квадрата равна произведению двух его смежных сторон", это утверждение верно. Думаю, комментариев не требуется.
2) "Диагональ
трапеции делит её на два равных треугольника." Во-первых, нет такого
свойства трапеции. 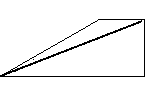 Во-вторых, если рассмотреть
прямоугольную трапецию с
проведенной диагональю, то становится очевидным, что один из получившихся треугольников -
прямоугольный, а второй - нет.
Следовательно, это утверждение неверно.
Во-вторых, если рассмотреть
прямоугольную трапецию с
проведенной диагональю, то становится очевидным, что один из получившихся треугольников -
прямоугольный, а второй - нет.
Следовательно, это утверждение неверно.
3) "Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны", это утверждение неверно, т.к. не соответствует ни одному из
признаков равенства треугольников.
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
 Площадь равнобедренного треугольника равна 144√
Площадь равнобедренного треугольника равна 144√
 Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
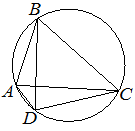 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.

Комментарии: