Лестница соединяет точки A и B и состоит из 15 ступеней. Высота каждой ступени равна 28 см, а длина – 96 см. Найдите расстояние между точками A и B (в метрах).
Каждая ступенька представляет из себя
прямоугольный треугольник, следовательно расстояние между точками А и В будет равняться сумме гипотенуз ступеней.
По
теореме Пифагора:
Квадрат гипотенузы ступени равен 282+962=784+9216=10000
Тогда длина гипотенузы равна √
Ответ: 15
Поделитесь решением
Присоединяйтесь к нам...
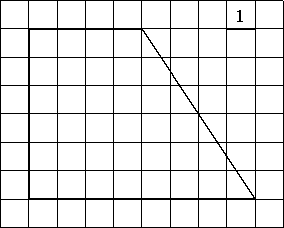Найдите площадь трапеции, изображённой на рисунке.
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 20, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
В треугольнике ABC угол C равен 90°, AC=10, tgA=0,1. Найдите BC.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
Центральный угол AOB равен
60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 7.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: