
 Площадь прямоугольного треугольника равна 8√
Площадь прямоугольного треугольника равна 8√
 Площадь
прямоугольного треугольника равна половине произведения катетов:
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2=8√
Пусть 60-и градусам равен угол ABC.
Тангенс ABC:
td∠ABC=tg60°=AC/BC=√
BC=AC/√
S=AC*BC/2=8√
AC*BC=16√
AC*AC/√
AC2=16√
AC=4
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
 К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOD.
 Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
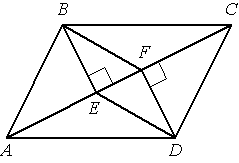 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ равны.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ равны.
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.

Комментарии:
(2017-09-07 16:39:45) Администратор: Катя, с какого места решения Вам непонятно?
(2017-09-07 15:29:24) Катя: Я не поняла задачу ,можно более развернутое решение .