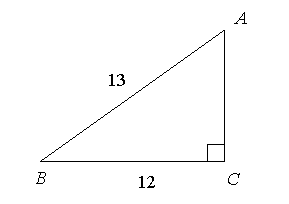
Найдите площадь треугольника, изображённого на рисунке.
Запомнить, формулу площади
прямоугольного треугольника очень легко.
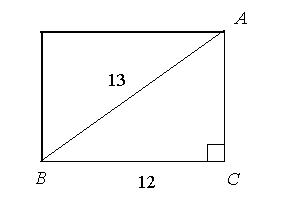
Надо зрительно дорисовать треугольник до
прямоугольника, площадь прямоугольника равна произведению его боковых сторон. В данном случае AC*BC. А площадь треугольника составляет ровно половину площади прямоугольника, т.е. S=AC*BC/2
Найдем AC по
теореме Пифагора:
AB2=AC2+BC2
132=AC2+122
AC2=169-144=25
AC=5
SABC=5*12/2=30
Ответ: SABC=30
Поделитесь решением
Присоединяйтесь к нам...
Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Основания BC и AD трапеции ABCD равны соответственно 5 и 45, BD=15. Докажите, что треугольники CBD и BDA подобны.
В треугольнике ABC угол C равен 90°, AC=12 , tgA=2√
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-24 17:24:52) Администратор: Андрей, но это же на много больше вычислений...
(2015-05-24 13:15:54) Андрей: Также эту задачу можно решить через теорему Герона.Найти полупериметр и дальше как по маслу)
(2015-05-17 23:54:55) Администратор: Иван, будьте корректны в выражениях. К тому же, непонятно, к кому Вы обращаетесь...к авторам сайта или к пользователям.
(2015-05-17 22:28:12) Иван: вы идиоты? площадь равна 1/2AC*BC
(2015-02-06 19:37:53) Администратор: Н, бывает )))
(2015-02-06 19:11:37) Н.: Извиняюсь, рисунок построила не так :D
(2015-02-06 19:08:55) Н.: Вы, действительно, уверенны в правильности данной задачи?! Площадь ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА можно найти, как половине произведения катетов! Значит, (12*13)/2=78. Площадь равна 78!