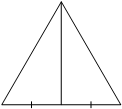
Медиана равностороннего треугольника равна 13√3. Найдите его сторону.
Вариант №1
По свойству равностороннего треугольника медиана равна (√3/2)*a, тогда:
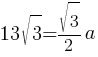
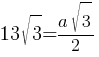
2*13√3=a√3
26√3=a√3
a=26
Ответ: 26
Поделитесь решением
Присоединяйтесь к нам...
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Центральный угол
AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
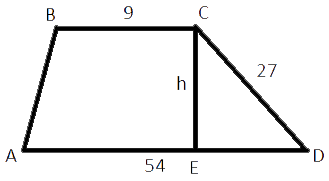Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен √
Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Средняя линия трапеции равна сумме её оснований.
3) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
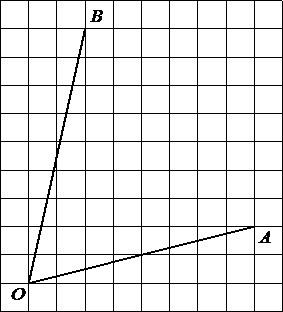Найдите тангенс угла
AOB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: