Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:2, KM=23.
Рассмотрим треугольники ABC и KBM.
∠B - общий.
∠BAC=∠BKM (т.к. это
соответственные углы)
∠BCA=∠BMK (т.к. это тоже
соответственные углы)
Следовательно, эти треугольники
подобны по
первому признаку подобия.
Тогда по
определению подобных треугольников:
BA/BK=AC/KM
(BK+KA)/BK=AC/KM
1+KA/BK=AC/KM
1+2/1=AC/23
3=AC/23
AC=3*23=69
Ответ: AC=69
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=14.
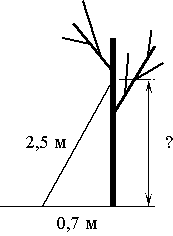Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
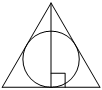Радиус окружности, вписанной в равносторонний треугольник, равен 12. Найдите высоту этого треугольника.
Лестница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
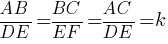
Комментарии: