
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Площадь прямоугольного треугольника S=AC*BC/2
Найдем AC по
теореме Пифагора:
AB2=AC2+BC2
452=AC2+362
AC2=2025-1296=729
AC=27
SABC=27*36/2=27*18=486
Ответ: SABC=486
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
 В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
 Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
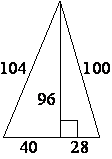 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?

Комментарии: