
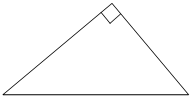
 Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
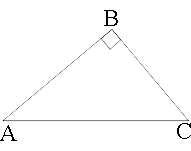 Введем обозначения как показано на рисунке.
Введем обозначения как показано на рисунке.
AB и BC - катеты, AC -
гипотенуза.
По
теореме Пифагора:
AC2=AB2+BC2
AC2=122+162
AC2=144+256
AC2=400
AC=√400=20
Ответ: 20
Поделитесь решением
Присоединяйтесь к нам...
 Точка H является основанием высоты
BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
Точка H является основанием высоты
BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
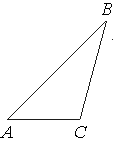 В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
 Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
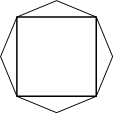 Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.

Комментарии: