Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Вариант №1 (Для тех, кто помним формулу)
По
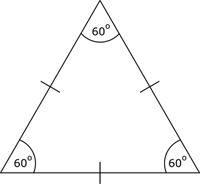
третьему свойству равностороннего треугольника:
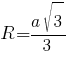
3R=a√3
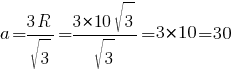
Ответ: 30
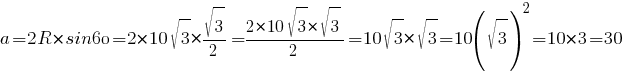
Поделитесь решением
Присоединяйтесь к нам...
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AMB.
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
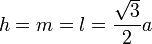
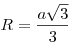
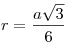
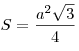
Комментарии: