
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ700 –Є–Ј 1087 |
 –Э–∞–є–і–Є—В–µ –Њ—Б—В—А—Л–µ —Г–≥–ї—Л –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –µ—Б–ї–Є –µ–≥–Њ –≥–Є–њ–Њ—В–µ–љ—Г–Ј–∞ —А–∞–≤–љ–∞ 20, –∞ –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–∞ 50√
–Э–∞–є–і–Є—В–µ –Њ—Б—В—А—Л–µ —Г–≥–ї—Л –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –µ—Б–ї–Є –µ–≥–Њ –≥–Є–њ–Њ—В–µ–љ—Г–Ј–∞ —А–∞–≤–љ–∞ 20, –∞ –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–∞ 50√
–†–µ—И–µ–љ–Є–µ –њ—А–Є—Б–ї–∞–ї –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—М –Ы—О–і–Љ–Є–ї–∞
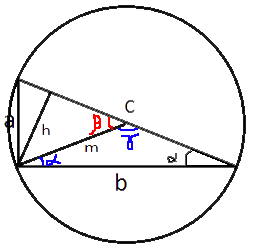 –Я—А–Њ–≤–µ–і–µ–Љ –Є–Ј –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ –Љ–µ–і–Є–∞–љ—Г –Є –≤—Л—Б–Њ—В—Г, –Њ–±–Њ–Ј–љ–∞—З–Є–≤ –Є—Е m –Є h —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.
–Я—А–Њ–≤–µ–і–µ–Љ –Є–Ј –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ –Љ–µ–і–Є–∞–љ—Г –Є –≤—Л—Б–Њ—В—Г, –Њ–±–Њ–Ј–љ–∞—З–Є–≤ –Є—Е m –Є h —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.
–Х—Б–ї–Є –Њ–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –≤–Њ–Ї—А—Г–≥ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —В–Њ —Ж–µ–љ—В—А —Н—В–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –±—Г–і–µ—В –ї–µ–ґ–∞—В—М –љ–∞ —Б–µ—А–µ–і–Є–љ–µ –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Л (–њ–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ–± –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є). –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ:
m=c/2=20/2=10
S=(1/2)hc => h=2S/c=2*50√
–Я–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О —Б–Є–љ—Г—Б–∞:
sinβ=h/m=5√
–Я–Њ —В–∞–±–ї–Є—Ж–µ –Њ–њ—А–µ–і–µ–ї—П–µ–Љ, —З—В–Њ β=45¬∞
–£–≥–Њ–ї γ —П–≤–ї—П–µ—В—Б—П –≤–љ–µ—И–љ–µ–Љ –Ї β, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ γ=180¬∞-β=180¬∞-45¬∞=135¬∞
–Ґ—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, —Б–Њ–і–µ—А–ґ–∞—Й–Є–є —Г–≥–Њ–ї γ,
—А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є, —В–∞–Ї –Ї–∞–Ї –Љ–µ–і–Є–∞–љ–∞ m –Є –њ–Њ–ї–Њ–≤–Є–љ–∞ –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Л —А–∞–≤–љ—Л (—Н—В–Њ –Љ—Л –≤—Л—П—Б–љ–Є–ї–Є —А–∞–љ–µ–µ).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —Г–≥–ї—Л –њ—А–Є –Њ—Б–љ–Њ–≤–∞–љ–Є–Є —А–∞–≤–љ—Л (–Њ–±–Њ–Ј–љ–∞—З–µ–љ—Л α).
–Ґ–Њ–≥–і–∞, –њ–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ —Б—Г–Љ–Љ–µ —Г–≥–ї–Њ–≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞:
180¬∞=γ+α+α
180¬∞=135¬∞+2α
α=22,5¬∞ - —Н—В–Њ –Њ–і–Є–љ –Є–Ј –Є—Б–Ї–Њ–Љ—Л—Е —Г–≥–ї–Њ–≤.
–Ф—А—Г–≥–Њ–є –Є—Б–Ї–Њ–Љ—Л–є —Г–≥–Њ–ї –љ–∞–є–і–µ–Љ –њ–Њ —В–Њ–є –ґ–µ
—В–µ–Њ—А–µ–Љ–µ –Њ–± —Г–≥–ї–∞—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞: 180¬∞-90¬∞-22,5¬∞=67,5¬∞
–Њ—В–≤–µ—В: 22,5¬∞ –Є 67,5¬∞
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
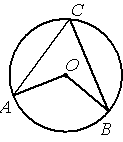 –Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /AOB=128¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ ACB (–≤ –≥—А–∞–і—Г—Б–∞—Е).
–Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /AOB=128¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ ACB (–≤ –≥—А–∞–і—Г—Б–∞—Е).
 –С–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ A –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Г BC –≤ —В–Њ—З–Ї–µ K. –Э–∞–є–і–Є—В–µ –њ–µ—А–Є–Љ–µ—В—А –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є BK=7, CK=12.
–С–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ A –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Г BC –≤ —В–Њ—З–Ї–µ K. –Э–∞–є–і–Є—В–µ –њ–µ—А–Є–Љ–µ—В—А –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є BK=7, CK=12.
 –¶–µ–љ—В—А–∞–ї—М–љ—Л–є —Г–≥–Њ–ї
AOB —А–∞–≤–µ–љ 60¬∞. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Е–Њ—А–і—Л AB, –љ–∞ –Ї–Њ—В–Њ—А—Г—О –Њ–љ –Њ–њ–Є—А–∞–µ—В—Б—П, –µ—Б–ї–Є —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 5.
–¶–µ–љ—В—А–∞–ї—М–љ—Л–є —Г–≥–Њ–ї
AOB —А–∞–≤–µ–љ 60¬∞. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Е–Њ—А–і—Л AB, –љ–∞ –Ї–Њ—В–Њ—А—Г—О –Њ–љ –Њ–њ–Є—А–∞–µ—В—Б—П, –µ—Б–ї–Є —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 5.
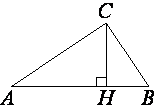 –Т –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Ї–∞—В–µ—В AC=65, –∞ –≤—Л—Б–Њ—В–∞ CH, –Њ–њ—Г—Й–µ–љ–љ–∞—П –љ–∞ –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Г, —А–∞–≤–љ–∞ 13√
–Т –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Ї–∞—В–µ—В AC=65, –∞ –≤—Л—Б–Њ—В–∞ CH, –Њ–њ—Г—Й–µ–љ–љ–∞—П –љ–∞ –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Г, —А–∞–≤–љ–∞ 13√
–Ю—Б–љ–Њ–≤–∞–љ–Є–µ AC —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ–Њ 10. –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —А–∞–і–Є—Г—Б–∞ 6 —Б —Ж–µ–љ—В—А–Њ–Љ –≤–љ–µ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Ї–∞—Б–∞–µ—В—Б—П –њ—А–Њ–і–Њ–ї–ґ–µ–љ–Є—П –±–Њ–Ї–Њ–≤—Л—Е —Б—В–Њ—А–Њ–љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Є –Ї–∞—Б–∞–µ—В—Б—П –Њ—Б–љ–Њ–≤–∞–љ–Є—П AC –≤ –µ–≥–Њ —Б–µ—А–µ–і–Є–љ–µ. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABC.

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: