В треугольнике ABC известно, что AB=BC, ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.
Так как, по условию, AB=BC, то данный треугольник называется равнобедренным.
По
первому свойству равнобедренного треугольника углы, противолежащие равным сторонам, равны между собой (обозначим их α).
Тогда по теореме о сумме углов треугольника:
180°=∠ABC+∠BCA+∠CAB
180°=102°+∠α+∠α
180°-102°=2∠α
78°=2∠α
∠α=78°/2=39°
Ответ: 39
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
Укажите номера верных утверждений.
1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.
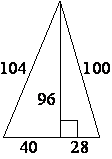Найдите площадь треугольника, изображённого на рисунке.
Сторона ромба равна 24, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: