На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
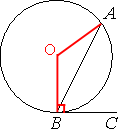Проведем отрезки из центра окружности к точкам А и В, как показано на рисунке.
∠AOB - центральный, следовательно равен градусной мере дуги, т.е. ∠AOB=92°.
Рассмотрим треугольник OAB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник
равнобедренный.
Следовательно, ∠OAB=∠OBA=x (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠AOB+∠OAB+∠OBA
180°=92°+x+x
2x=88°
x=44°
∠OBC=90° (по
свойству касательной).
∠ABC=∠OBC-∠OBA
∠ABC=90°-44°
∠ABC=46°
Ответ: 46
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
3) Площадь круга меньше квадрата длины его диаметра.
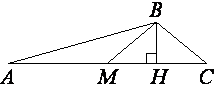В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64, HC=16 и ∠ACB=37°. Найдите угол AMB. Ответ дайте в градусах.
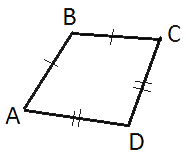В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
В трапецию, сумма длин боковых сторон которой равна 16, вписана окружность. Найдите длину средней линии трапеции.
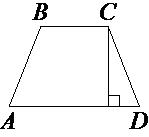Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-10-09 20:18:09) Администратор: meltdown, как?
(2019-10-09 20:09:23) meltdown: помогите пожалуйста
(2017-05-14 18:59:05) Администратор: Людмила, в математике утверждений не бывает. Бывают определения, теоремы и аксиомы. Поэтому при решении или надо ссылаться на определения, теоремы и аксиомы, или доказывать.
(2017-05-13 18:50:59) Людмила: Можно просто воспользоваться утверждением, что угол между хордой и касательной равен половине дуги, заключенной внутри него. Доказывать это не обязательно