Сторона AB параллелограмма ABCD вдвое больше стороны AD.
Точка L — середина стороны AB. Докажите, что DL — биссектриса
угла ADC.
Рассмотрим треугольник ALD.
AL вдвое меньше AB (по условию задачи).
AD тоже вдвое меньше AB (по условию задачи), следовательно:
AL=AD
Т.е. данный треугольник
равнобедренный.
По
свойству равнобедренного треугольника ∠ADL=∠ALD
∠ALD=∠LDC (т.к. это
накрест-лежащие углы).
Получается, что ∠ADL=∠LDC.
Следовательно DL -
биссектриса.
Поделитесь решением
Присоединяйтесь к нам...
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.
Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
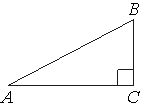В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: