Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
OK перпендикулярен к
касательной (по
свойству касательной), т.е. угол между OK и
касательной равен 90°.
Следовательно, ∠OKM=90°-7°=83°
Треугольник OMK -
равнобедренный (т.к. OM и OK - радиусы окружности и, соответственно, равны друг другу).
По
свойству равнобедренного треугольника ∠OKM=∠OMK=83°
Ответ: ∠OMK=83°
Поделитесь решением
Присоединяйтесь к нам...
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=34.
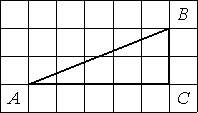Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.
2) Существует параллелограмм, который не является прямоугольником.
3) Сумма углов тупоугольного треугольника равна 180°.
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: