Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=122° и ∠ACB=47°. Найдите угол DCB. Ответ дайте в градусах.
Рассмотрим треугольник ACD.
По
теореме о сумме углов треугольника:
180°=∠CAB+∠ADC+∠ACD
180°=122°+∠ADC+∠ACD
∠ADC+∠ACD=58°
Так как AD=AC, то данный треугольник
равнобедренный.
Тогда, ∠ADC=∠ACD (по
свойству равнобедренного треугольника), получаем, что:
∠ADC=∠ACD=58°/2=29°
∠DCB=∠ACB-∠ACD=47°-29°=18°
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
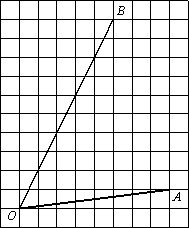Найдите тангенс угла AOB.
Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
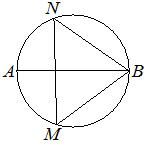На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
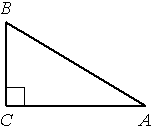В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
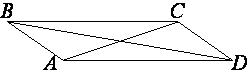В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: