
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ610 –Є–Ј 1087 |
 –Ш–Ј –≤–µ—А—И–Є–љ—Л –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ C —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –≤—Л—Б–Њ—В–∞ CP. –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BCP, —А–∞–≤–µ–љ 60, —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ BAC —А–∞–≤–µ–љ 5/12. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABC.
–Ш–Ј –≤–µ—А—И–Є–љ—Л –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ C —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –≤—Л—Б–Њ—В–∞ CP. –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BCP, —А–∞–≤–µ–љ 60, —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ BAC —А–∞–≤–µ–љ 5/12. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABC.
–Т–∞—А–Є–∞–љ—В вДЦ1
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABC –Є BCP.
∠ABC - –Њ–±—Й–Є–є.
∠ACB=∠BPC=90¬∞ (—В.–Ї. CP -
–≤—Л—Б–Њ—В–∞).
–Я–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г –њ–Њ–і–Њ–±–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤, –і–∞–љ–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є
–њ–Њ–і–Њ–±–љ—Л.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, BC/AC=BP/BC=BC/AB=k.
k - –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –њ–Њ–і–Њ–±–Є—П.
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ BC/AB - —Н—В–Њ sinA (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О), –љ–∞–є–і–µ–Љ –µ–≥–Њ:
tgA=(sinA)/(cosA)=5/12
cosA=(12sinA)/5=2,4sinA
–Я–Њ –Њ—Б–љ–Њ–≤–љ–Њ–є —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є —Д–Њ—А–Љ—Г–ї–µ:
sin2A+cos2A=1
sin2A+(2,4sinA)2=1
sin2A+5,76sin2A=1
6,76sin2A=1
sin2A=1/6,76
sinA=1/2,6=k
–Ф–∞–ї—М—И–µ —В–Њ–љ–Ї–Є–є –Љ–Њ–Љ–µ–љ—В:
–Я–Њ —Б–≤–Њ–є—Б—В–≤—Г –њ–Њ–і–Њ–±–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–µ—А–Є–Љ–µ—В—А–Њ–≤ –Є –і–ї–Є–љ –±–Є—Б—Б–µ–Ї—В—А–Є—Б, –Љ–µ–і–Є–∞–љ, –≤—Л—Б–Њ—В –Є —Б–µ—А–µ–і–Є–љ–љ—Л—Е –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–Њ–≤ —А–∞–≤–љ–Њ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Г –њ–Њ–і–Њ–±–Є—П.
–†–∞–і–Є—Г—Б
–≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –Є–Љ–µ–µ—В –ї–Є–љ–µ–є–љ—Г—О –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М –Њ—В –њ–µ—А–Є–Љ–µ—В—А–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ (
—В—А–µ—В—М–µ —Б–≤–Њ–є—Б—В–≤–Њ), —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ —А–∞–і–Є—Г—Б–Њ–≤ –њ–Њ–і–Њ–±–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ —В–Њ–ґ–µ –њ–Њ–і—З–Є–љ—П–µ—В—Б—П –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Г –њ–Њ–і–Њ–±–Є—П.
–Ґ.–µ. r/R=k
R=r/k=60/(1/2,6)=60*2,6=156.
–Ю—В–≤–µ—В: R=156
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
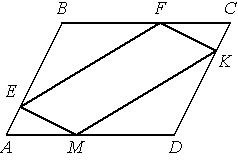 –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ –Р–Т–°D —В–Њ—З–Ї–Є E, F, K –Є –Ь –ї–µ–ґ–∞—В –љ–∞ –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞—Е, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ, –њ—А–Є—З—С–Љ –Р–Х = CK, BF = DM. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ EFKM вАФ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ –Р–Т–°D —В–Њ—З–Ї–Є E, F, K –Є –Ь –ї–µ–ґ–∞—В –љ–∞ –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞—Е, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ, –њ—А–Є—З—С–Љ –Р–Х = CK, BF = DM. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ EFKM вАФ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ.
 –Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ 60¬∞, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю —А–∞–≤–љ–Њ 8.
–Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ 60¬∞, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю —А–∞–≤–љ–Њ 8.
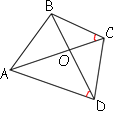 –Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABCD —Г–≥–ї—Л BCA –Є BDA —А–∞–≤–љ—Л. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —Г–≥–ї—Л ABD –Є ACD —В–∞–Ї–ґ–µ —А–∞–≤–љ—Л.
–Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABCD —Г–≥–ї—Л BCA –Є BDA —А–∞–≤–љ—Л. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —Г–≥–ї—Л ABD –Є ACD —В–∞–Ї–ґ–µ —А–∞–≤–љ—Л.
 –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O –Њ–њ–Є—Б–∞–љ–∞ –Њ–Ї–Њ–ї–Њ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –≤ –Ї–Њ—В–Њ—А–Њ–Љ AB=BC –Є ∠ABC=79¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BOC. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O –Њ–њ–Є—Б–∞–љ–∞ –Њ–Ї–Њ–ї–Њ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –≤ –Ї–Њ—В–Њ—А–Њ–Љ AB=BC –Є ∠ABC=79¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BOC. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Ю—Б–љ–Њ–≤–∞–љ–Є—П BC –Є AD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 5 –Є 20, BD=10. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є CBD –Є BDA –њ–Њ–і–Њ–±–љ—Л.
–Ю—Б–љ–Њ–≤–∞–љ–Є—П BC –Є AD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 5 –Є 20, BD=10. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є CBD –Є BDA –њ–Њ–і–Њ–±–љ—Л.





–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2015-04-12 17:00:19) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: AB2=144*CB2/25+CB2=144*CB2/25+25CB2/25=(144CB2+25CB2)/25=169CB2/25
(2015-04-12 16:52:31) : AB2=144*CB2/25+CB2 AB2=169*CB2/25 –њ–Њ—З–µ–Љ—Г –Є—Б—З–µ–Ј–ї–Њ CB?
(2015-03-18 20:20:21) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Т—Б–µ–≤–Њ–ї–Њ–і, –љ–∞–њ–Є—И–Є—В–µ, –Љ–љ–µ –њ–Њ–ґ–∞–ї—Г–є—Б—В–∞, –љ–∞ zapros@otvet-gotov.ru, –і–∞–≤–∞–є—В–µ –і–Є—Б–Ї—Г—В–Є—А–Њ–≤–∞—В—М –њ–Њ –њ–Њ—З—В–µ, —З—В–Њ–±—Л –љ–µ "–≤–Ј—А—Л–≤–∞—В—М –Љ–Њ–Ј–≥" –і—А—Г–≥–Є–Љ –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—П–Љ )
(2015-03-18 20:14:32) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Т—Б–µ–≤–Њ–ї–Њ–і, –±–Њ–ї—М—И–Њ–µ –Т–∞–Љ —Б–њ–∞—Б–Є–±–Њ –Ј–∞ —В–∞–Ї—Г—О —Г–њ–Њ—А–љ—Г—О –±–Њ—А—М–±—Г –Ј–∞ –Є—Б—В–Є–љ—Г. –Ф–Є—Б–Ї—Г—В–Є—А–Њ–≤–∞—В—М —Б —В–∞–Ї–Є–Љ –Њ–њ–њ–Њ–љ–µ–љ—В–Њ–Љ - –Њ–і–љ–Њ —Г–і–Њ–≤–Њ–ї—М—Б—В–≤–Є–µ. –Т —З–µ–Љ —П —Б –Т–∞–Љ–Є —Б–Њ–≥–ї–∞—Б–µ–љ, —В–∞–Ї —Н—В–Њ –≤ —В–Њ–Љ, —З—В–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–љ–∞—П –Љ–љ–Њ–є —Д–Њ—А–Љ—Г–ї–∞ –Љ–∞–ї–Њ –Є–Ј–≤–µ—Б—В–љ–∞ –Є, –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ, —В—А–µ–±—Г–µ—В –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–∞. –Ґ.–µ. –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –µ–µ –Ї–∞–Ї –µ—Б—В—М –љ–µ –Њ—З–µ–љ—М –Ї–Њ—А—А–µ–Ї—В–љ–Њ –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ. –Э–Њ –Є–Љ–µ–љ–љ–Њ –њ–Њ —Н—В–Њ–є –ґ–µ –њ—А–Є—З–Є–љ–µ, –љ–µ–Ї–Њ—А—А–µ–Ї—В–љ–Њ —Г—В–≤–µ—А–ґ–і–∞—В—М, —З—В–Њ R/r=k, —Н—В–Њ –љ–∞–і–Њ –њ–Њ–Ї–∞–Ј–∞—В—М. –Ь—Л —Б –Т–∞–Љ–Є –њ–Њ–љ–Є–Љ–∞–µ–Љ, —З—В–Њ –≤—Л—Б–Њ—В—Л, –Љ–µ–і–Є–∞–љ—Л –Є —В.–і. "–њ–Њ–і—З–Є–љ—П—О—В—Б—П" –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Г –њ–Њ–і–Њ–±–Є—П, –њ–ї–Њ—Й–∞–і–Є –њ–Њ–і–Њ–±–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ —Г–ґ–µ "–љ–µ –њ–Њ–і—З–Є–љ—П—О—В—Б—П". –Ф–ї—П –Њ–±—Л—З–љ–Њ–≥–Њ —И–Ї–Њ–ї—М–љ–Є–Ї–∞ —Н—В–Є —В–Њ–љ–Ї–Њ—Б—В–Є –љ–µ –Њ—З–µ–≤–Є–і–љ—Л. –Т—Л –Љ–µ–љ—П —Г–±–µ–і–Є–ї–Є, —З—В–Њ –љ–∞–і–Њ –љ–∞–њ–Є—Б–∞—В—М –±–Њ–ї–µ–µ –Ї–Њ—А—А–µ–Ї—В–љ–Њ–µ —А–µ—И–µ–љ–Є–µ. –ѓ —Н—В–Є–Љ –Ј–∞–є–Љ—Г—Б—М –љ–µ–Љ–љ–Њ–≥–Њ –њ–Њ–Ј–ґ–µ, —Б–µ–є—З–∞—Б –Њ—З–µ–љ—М –Љ–љ–Њ–≥–Њ –Ј–∞–њ—А–Њ—Б–Њ–≤ –љ–∞ –љ–Њ–≤—Л–µ –Ј–∞–і–∞—З–Є. –Х—Й–µ —А–∞–Ј —Б–њ–∞—Б–Є–±–Њ –Т–∞–Љ!
(2015-03-18 13:26:43) –Т—Б–µ–≤–Њ–ї–Њ–і: –Т —Г—З–µ–±–љ–Є–Ї–µ –Р.–Т.–Я–Њ–≥–Њ—А–µ–ї–Њ–≤–∞ –љ–∞ —Б—В—А. 154 –µ—Б—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ –њ–Њ–і–Њ–±–Є—П –Ї–∞–Ї –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П, –∞ –њ–Њ—В–Њ–Љ –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —Б—В—А–∞–љ–Є—Ж –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –њ–Њ–і—А–Њ–±–љ–Њ –≥–Њ–≤–Њ—А–Є—В—Б—П –Њ –µ–≥–Њ —Б–≤–Њ–є—Б—В–≤–∞—Е –Є –њ—А–Є–≤–Њ–і—П—В—Б—П —Е–Њ—А–Њ—И–Є–µ –њ—А–Є–Љ–µ—А—Л. –Т —Г—З–µ–±–љ–Є–Ї–µ –њ–Њ–і —А–µ–і–∞–Ї—Ж–Є–µ–є –Р.–Э.–Ґ–Є—Е–Њ–љ–Њ–≤–∞ –љ–∞ —Б—В—А. 138 –Њ –њ–Њ–і–Њ–±–Є–Є —Б–Ї–∞–Ј–∞–љ–Њ –ї–Є—И—М: "–Т –≥–µ–Њ–Љ–µ—В—А–Є–Є —Д–Є–≥—Г—А—Л –Њ–і–Є–љ–∞–Ї–Њ–≤–Њ–є —Д–Њ—А–Љ—Л –њ—А–Є–љ—П—В–Њ –љ–∞–Ј—Л–≤–∞—В—М –њ–Њ–і–Њ–±–љ—Л–Љ–Є". –Ф—А—Г–≥–Є–µ —Г—З–µ–±–љ–Є–Ї–Є –љ–µ —Б–Љ–Њ—В—А–µ–ї, –љ–Њ –і–Њ–њ—Г—Б–Ї–∞—О, —З—В–Њ –Њ–љ–Є –Љ–Њ–≥—Г—В —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ —А–∞–Ј–ї–Є—З–∞—В—М—Б—П. –Т –Ъ–Њ–і–Є—Д–Є–Ї–∞—В–Њ—А–µ —Н–ї–µ–Љ–µ–љ—В–Њ–≤ –§–Ш–Я–Ш –µ—Б—В—М –њ—Г–љ–Ї—В 7.1.6 "–Я—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є. –Ф–≤–Є–ґ–µ–љ–Є—П. –°–Є–Љ–Љ–µ—В—А–Є—П." –Ф–∞, —Б–Ї–∞–Ј–∞–љ–Њ –Љ–∞–ї–Њ, –љ–Њ —Н—В–Њ –њ—А–Њ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ –њ–Њ–і–Њ–±–Є—П. –Ь–љ–µ –Ї–∞–ґ–µ—В—Б—П, —З—В–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е —А–∞–і–Є—Г—Б–Њ–≤ –Є –≤—Л—Б–Њ—В —Г –њ–Њ–і–Њ–±–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –і–Њ–Ї–∞–Ј—Л–≤–∞—В—М –љ–µ –љ–∞–і–Њ –њ–Њ—В–Њ–Љ—Г, —З—В–Њ —Н—В–Њ —П–≤–ї—П–µ—В—Б—П –Њ–і–љ–Є–Љ –Є–Ј –Њ—Б–љ–Њ–≤–љ—Л—Е —Б–≤–Њ–є—Б—В–≤ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П –њ–Њ–і–Њ–±–Є—П. –°–Њ–≥–ї–∞—Б–µ–љ —Б —В–µ–Љ, —З—В–Њ –љ–∞ —Г—З–µ–±–љ–Є–Ї–Є, –Ї–Њ—В–Њ—А—Л–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—О—В —Б—А–∞–Ј—Г –ї–Є—И—М –њ—А–Є–Ј–љ–∞–Ї–Є –њ–Њ–і–Њ–±–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –±–µ–Ј —Г–њ–Њ–Љ–Є–љ–∞–љ–Є—П –Њ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–Є –њ–Њ–і–Њ–±–Є—П —В–∞–Ї –Њ–њ–µ—А–µ—В—М—Б—П –љ–µ –њ–Њ–ї—Г—З–Є—В—Б—П. –Х—Б–ї–Є —Б—З–Є—В–∞—В—М, —З—В–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ –њ–Њ–і–Њ–±–Є—П –Ї–∞–Ї –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П –≤ –њ—А–Њ–≥—А–∞–Љ–Љ–µ –Є —Г—З–µ–±–љ–Є–Ї–∞—Е –Њ—В—Б—Г—В—Б—В–≤—Г–µ—В, —В–Њ –≤—Л –њ—А–∞–≤—Л, –љ—Г–ґ–љ–Њ –≥–Њ–љ—П—В—М –Є–Ј–≤–µ—Б—В–љ—Л–µ —Д–Њ—А–Љ—Г–ї—Л. –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ S=(b*c*sinA)/2 (–µ—Й–µ –њ–Њ–і–Њ–є–і—С—В —Д–Њ—А–Љ—Г–ї–∞ –У–µ—А–Њ–љ–∞, –љ–Њ —Б –њ—А–Њ–≤–µ—А–Ї–Њ–є –≤—Б–µ—Е —Г—З–µ–±–љ–Є–Ї–Њ–≤). –Ш–Ј –љ–µ—С –≤—Л—Е–Њ–і–Є—В, —З—В–Њ –њ–ї–Њ—Й–∞–і–Є –њ–Њ–і–Њ–±–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –Њ—В–љ–Њ—Б—П—В—Б—П –Ї–∞–Ї –Ї–≤–∞–і—А–∞—В –Є—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞ –њ–Њ–і–Њ–±–Є—П –Є –Њ–± —Н—В–Њ–Љ –≥–Њ–≤–Њ—А–Є—В—Б—П –≤–µ–Ј–і–µ. –Ґ–Њ–≥–і–∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–µ —А–∞–і–Є—Г—Б—Л –Є –≤—Л—Б–Њ—В—Л —В–Њ–ґ–µ –њ–Њ–і–Њ–±–љ—Л —Б —В–µ–Љ –ґ–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–Љ, –њ–Њ—В–Њ–Љ—Г —З—В–Њ –≤–µ–Ј–і–µ –µ—Б—В—М —Д–Њ—А–Љ—Г–ї—Л –і–ї—П –њ–ї–Њ—Й–∞–і–Є S=a*b*c/4R, S=p*r –Є S=a*h/2. –Т—Л –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Є –≤ —А–µ—И–µ–љ–Є–Є —Д–Њ—А–Љ—Г–ї—Г r=(a+b-c)/2, —Г–њ–Њ–Љ–Є–љ–∞–љ–Є–µ –Њ –Ї–Њ—В–Њ—А–Њ–є –љ–µ —В–∞–Ї –њ—А–Њ—Б—В–Њ –±—Г–і–µ—В –љ–∞–є—В–Є –≤ –љ–µ–Ї–Њ—В–Њ—А—Л—Е —Г—З–µ–±–љ–Є–Ї–∞—Е. –Т–Њ–Њ–±—Й–µ, –≤—Б–µ–≥–і–∞ –Љ–Њ–ґ–љ–Њ –њ–Њ–њ—А–Њ—Б–Є—В—М –і–Њ–Ї–∞–Ј–∞—В—М –≤—Б–µ –њ—А–Є–Љ–µ–љ—С–љ–љ—Л–µ –≤ —А–µ—И–µ–љ–Є–Є —Д–Њ—А–Љ—Г–ї—Л –Є —Г—В–≤–µ—А–ґ–і–µ–љ–Є—П. –Э–Њ —В–Њ–≥–і–∞ –љ–∞—З–Є–љ–∞—В—М –њ—А–Є–і—С—В—Б—П —Б "–Э–∞—З–∞–ї" –њ–ї–∞–љ–Є–Љ–µ—В—А–Є–Є –Є–ї–Є –Ј–∞—Й–Є—Й–∞—В—М—Б—П —Д—А–∞–Ј–Њ–є "–Є–Ј –њ—А–Њ–≥—А–∞–Љ–Љ—Л", –∞ —Н—В–Њ —Г–ґ–µ —Б—Г–±—Б—В–∞–љ—Ж–Є—П –і–Є—Б–Ї—Г—Б—Б–Є–Њ–љ–љ–∞—П. –Х—Б–ї–Є –ґ–µ —Б—З–Є—В–∞—В—М, —З—В–Њ –њ–Њ–љ—П—В–Є–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П –њ–Њ–і–Њ–±–Є—П –≤ –њ—А–Њ–≥—А–∞–Љ–Љ–µ –≤—Б—С –ґ–µ –µ—Б—В—М, —В–Њ —Б—Б—Л–ї–Ї–∞ –≤ —А–µ—И–µ–љ–Є–Є –љ–∞ –µ–≥–Њ —Б–≤–Њ–є—Б—В–≤–∞ –≤—Л–≥–ї—П–і–Є—В –Љ–Њ—Й–љ–µ–µ –Є –ї–µ–≥—З–µ, —З–µ–Љ –њ—А–Є–Љ–µ–љ–µ–љ–Є–µ –Є–Ј–≤–µ—Б—В–љ—Л—Е —Д–Њ—А–Љ—Г–ї.
(2015-03-09 16:23:33) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Т—Б–µ–≤–Њ–ї–Њ–і, –Т–∞—И–µ —А–µ—И–µ–љ–Є–µ –≤ —Ж–µ–ї–Њ–Љ –њ—А–∞–≤–Є–ї—М–љ–Њ–µ, –Ї—А–Њ–Љ–µ –Њ–і–љ–Њ–≥–Њ –Э–Ю. –Т—Л —Б—Б—Л–ї–∞–µ—В–µ—Б—М –љ–∞ —Б–≤–Њ–є "–ґ–Є–Ј–љ–µ–љ–љ—Л–є –Њ–њ—Л—В", –∞ –љ–µ –љ–∞ —В–µ–Њ—А–µ–Љ—Л –Є–ї–Є –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П "–Ю—В–љ–Њ—И–µ–љ–Є–µ —А–∞–і–Є—Г—Б–Њ–≤ –≤–њ–Є—Б–∞–љ–љ—Л—Е –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є —Г –њ–Њ–і–Њ–±–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ —В–Њ–ґ–µ —А–∞–≤–љ–Њ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Г –њ–Њ–і–Њ–±–Є—П". –≠—В–Њ –љ—Г–ґ–љ–Њ –і–Њ–Ї–∞–Ј–∞—В—М –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є, –∞ –љ–µ –≥–Њ–ї–Њ—Б–ї–Њ–≤–љ–Њ, –і–∞–ґ–µ, –µ—Б–ї–Є —Н—В–Њ –Њ—З–µ–≤–Є–і–љ–Њ. "–Т–µ–і—М –њ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ–Њ–і–Њ–±–Є—П –≤—Б–µ –ї–Є–љ–µ–є–љ—Л–µ —А–∞–Ј–Љ–µ—А—Л —Д–Є–≥—Г—А—Л —Г–≤–µ–ї–Є—З–Є–≤–∞—О—В—Б—П –≤ k —А–∞–Ј (—Б—В–Њ—А–Њ–љ—Л, –Љ–µ–і–Є–∞–љ—Л, –≤—Л—Б–Њ—В—Л, –±–Є—Б—Б–µ–Ї—В—А–Є—Б—Л, –і–Є–∞–≥–Њ–љ–∞–ї–Є –Є —А–∞–і–Є—Г—Б—Л –≤–њ–Є—Б–∞–љ–љ–Њ–є –Є –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є)" - –≤ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–Є –њ–Њ–і–Њ–±–Є—П –љ–Є—З–µ–≥–Њ –њ–Њ—Е–Њ–ґ–µ–≥–Њ –љ–µ—В. –Ю–Я–†.: –Я–Њ–і–Њ–±–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є вАФ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є, —Г –Ї–Њ—В–Њ—А—Л—Е —Г–≥–ї—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —А–∞–≤–љ—Л, –∞ —Б—В–Њ—А–Њ–љ—Л –Њ–і–љ–Њ–≥–Њ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ—Л —Б—В–Њ—А–Њ–љ–∞–Љ –і—А—Г–≥–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞. –Т—Б–µ –Њ—Б—В–∞–ї—М–љ–Њ–µ –љ–∞–і–Њ –і–Њ–Ї–∞–Ј—Л–≤–∞—В—М –≤ —А–µ—И–µ–љ–Є–Є...–Х—Б–ї–Є —П –љ–µ –њ—А–∞–≤, —В–Њ –њ—А–Є—И–ї–Є—В–µ, –њ–Њ–ґ–∞–ї—Г–є—Б—В–∞, —Б—Б—Л–ї–Ї—Г –љ–∞ –Љ–∞—В–µ—А–Є–∞–ї—Л, –≥–і–µ –њ–Њ–і—В–≤–µ—А–ґ–і–∞—О—В—Б—П –Т–∞—И–Є —Б–ї–Њ–≤–∞.
(2015-03-07 16:55:58) –Т—Б–µ–≤–Њ–ї–Њ–і: –Ґ—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є CBP –Є ABC –њ–Њ–і–Њ–±–љ—Л —Б –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–Љ –њ–Њ–і–Њ–±–Є—П k=BC/AB, –∞ —Н—В–Њ –≤–µ–і—М sinA. –Ш—Б–њ–Њ–ї—М–Ј—Г—П –Њ—Б–љ–Њ–≤–љ–Њ–µ —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ —В–Њ–ґ–і–µ—Б—В–≤–Њ –Є –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ tgA, –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є sinA –Є–Ј —Б–Є—Б—В–µ–Љ—Л: (sinA)^2+(cosA)^2=1 sinA/cosA=5/12=tgA –Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ sinA=5/13 –Ю—В–љ–Њ—И–µ–љ–Є–µ —А–∞–і–Є—Г—Б–Њ–≤ –≤–њ–Є—Б–∞–љ–љ—Л—Е –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є —Г –њ–Њ–і–Њ–±–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ —В–Њ–ґ–µ —А–∞–≤–љ–Њ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Г –њ–Њ–і–Њ–±–Є—П. –Т–µ–і—М –њ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ–Њ–і–Њ–±–Є—П –≤—Б–µ –ї–Є–љ–µ–є–љ—Л–µ —А–∞–Ј–Љ–µ—А—Л —Д–Є–≥—Г—А—Л —Г–≤–µ–ї–Є—З–Є–≤–∞—О—В—Б—П –≤ k —А–∞–Ј (—Б—В–Њ—А–Њ–љ—Л, –Љ–µ–і–Є–∞–љ—Л, –≤—Л—Б–Њ—В—Л, –±–Є—Б—Б–µ–Ї—В—А–Є—Б—Л, –і–Є–∞–≥–Њ–љ–∞–ї–Є –Є —А–∞–і–Є—Г—Б—Л –≤–њ–Є—Б–∞–љ–љ–Њ–є –Є –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є). –Ш—В–∞–Ї, —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ —А–∞–і–Є—Г—Б–Њ–≤ —Г –љ–∞—Б —А–∞–≤–љ–Њ r/R=5/13,–Њ—В–Ї—Г–і–∞ R=156.