
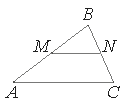
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=28. Площадь треугольника ABC равна 162. Найдите площадь треугольника MBN.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=28. Площадь треугольника ABC равна 162. Найдите площадь треугольника MBN.
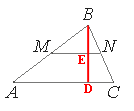 Проведем
высоту BD из вершины B.
Проведем
высоту BD из вершины B.
Площадь треугольника ABC:
SABC=BD*AC/2
162=BD*36/2
BD=162*2/36=9
Рассмотрим треугольники ABC и MBN.
∠B - общий.
∠BAC=∠BMN (так как это
соответственные углы).
Следовательно, данные треугольники
подобны (по двум углам).
Тогда, справедливо соотношение сторон и высот данных треугольников:
AC/MN=BD/BE
BE=MN*BD/AC=28*9/36=28/4=7
Площадь треугольника ABC:
SMBN=BE*MN/2=7*28/2=7*14=98
Ответ: 98
Поделитесь решением
Присоединяйтесь к нам...
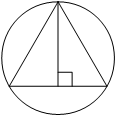 Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
 Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
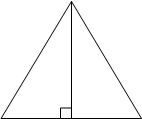 Высота равностороннего треугольника равна
15√
Высота равностороннего треугольника равна
15√
 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.



Комментарии:
(2019-01-19 12:02:26) Администратор: Алина, это условие задачи.
(2019-01-10 13:30:34) алина: как получилось 162?
(2017-05-14 18:51:30) Администратор: Людмила, а про отношение площадей подобных треугольников говорится в каком-нибудь учебнике?
(2017-05-13 18:42:00) Людмила: Можно короче: отношение площадей подобных треугольников равно коэффициенту подобия в квадрате. К=28/36 = 7/9, значит отношение площадей треугольников = 49/81 Тогда S = 162*(49/81) = 98