
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ427 –Є–Ј 1087 |
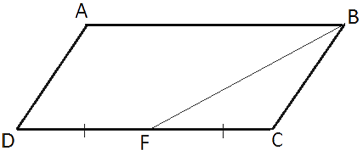 –°—В–Њ—А–Њ–љ–∞ CD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –≤–і–≤–Њ–µ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л BC. –Ґ–Њ—З–Ї–∞ F вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л CD. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ BF вАФ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ ABC.
–°—В–Њ—А–Њ–љ–∞ CD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –≤–і–≤–Њ–µ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л BC. –Ґ–Њ—З–Ї–∞ F вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л CD. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ BF вАФ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ ABC.
BC=CD/2=CF (–њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є)
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BCF -
—А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є.
–Я–Њ
—Б–≤–Њ–є—Б—В–≤—Г —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞:
∠CFB=∠CBF
∠CFB=∠ABF (—В–∞–Ї –Ї–∞–Ї —Н—В–Њ
–љ–∞–Ї—А–µ—Б—В-–ї–µ–ґ–∞—Й–Є–µ —Г–≥–ї—Л)
–Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ ∠CBF=∠ABF
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, BF -
–±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞.
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
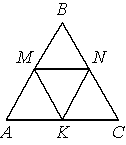 –Т —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —В–Њ—З–Ї–Є M, N, K вАФ —Б–µ—А–µ–і–Є–љ—Л —Б—В–Њ—А–Њ–љ –Р–Т, –Т–°, –°–Р —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –ТMKN вАФ —А–Њ–Љ–±.
–Т —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —В–Њ—З–Ї–Є M, N, K вАФ —Б–µ—А–µ–і–Є–љ—Л —Б—В–Њ—А–Њ–љ –Р–Т, –Т–°, –°–Р —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –ТMKN вАФ —А–Њ–Љ–±.
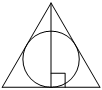 –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, —А–∞–≤–µ–љ 12. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, —А–∞–≤–µ–љ 12. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
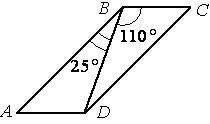 –Ф–Є–∞–≥–Њ–љ–∞–ї—М BD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ
25¬∞ –Є 110¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
–Ф–Є–∞–≥–Њ–љ–∞–ї—М BD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ
25¬∞ –Є 110¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
–Ъ–∞–Ї–Є–µ –Є–Ј –і–∞–љ–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є –≤–µ—А–љ—Л? –Ч–∞–њ–Є—И–Є—В–µ –Є—Е –љ–Њ–Љ–µ—А–∞.
1) –Э–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є —Б—Г—Й–µ—Б—В–≤—Г–µ—В –µ–і–Є–љ—Б—В–≤–µ–љ–љ–∞—П —В–Њ—З–Ї–∞, —А–∞–≤–љ–Њ—Г–і–∞–ї—С–љ–љ–∞—П –Њ—В –Ї–Њ–љ—Ж–Њ–≤ –Њ—В—А–µ–Ј–Ї–∞.
2) –Т –ї—О–±–Њ–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Љ–Њ–ґ–љ–Њ –≤–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М.
3) –Х—Б–ї–Є –≤ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ –і–≤–µ —Б–Љ–µ–ґ–љ—Л–µ —Б—В–Њ—А–Њ–љ—Л —А–∞–≤–љ—Л, —В–Њ —В–∞–Ї–Њ–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ —П–≤–ї—П–µ—В—Б—П —А–Њ–Љ–±–Њ–Љ.
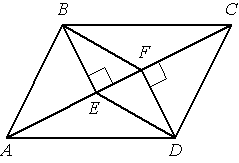 –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ –Р–Т–°D –њ—А–Њ–≤–µ–і–µ–љ—Л –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А—Л –Т–Х –Є DF –Ї –і–Є–∞–≥–Њ–љ–∞–ї–Є –Р–° (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –Њ—В—А–µ–Ј–Ї–Є –ТF –Є D–Х –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ –Р–Т–°D –њ—А–Њ–≤–µ–і–µ–љ—Л –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А—Л –Т–Х –Є DF –Ї –і–Є–∞–≥–Њ–љ–∞–ї–Є –Р–° (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –Њ—В—А–µ–Ј–Ї–Є –ТF –Є D–Х –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л.



–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2022-09-12 10:35:22) : –Р–Т = CD = 14 —Б–Љ, –Т–° = AD = 27 —Б–Љ –Ј–∞ –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—П–Љ–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ –† ABCD = –Р–Т + CD + –Т–° + AD –† ABCD = вА¶ –Т—Ц–і–њ–Њ–≤—Ц–і—М :