Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
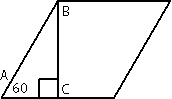Рассмотрим треугольник АВС.
Этот треугольник
прямоугольный (по условию задачи).
∠A=60°, следовательно по
теореме о сумме углов треугольника:
∠АВС = 180°-90°-60°=30°.
По второму свойству прямоугольного треугольника:
АС=АВ/2=32/2=16.
Следовательно вторая половина стороны ромба = 32-16=16.
Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: 16 и 16.
Поделитесь решением
Присоединяйтесь к нам...
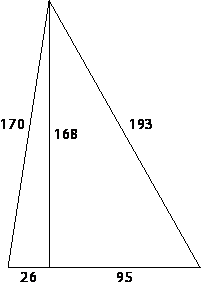Найдите площадь треугольника, изображённого на рисунке.
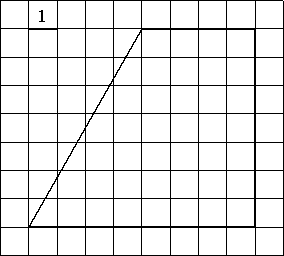Найдите площадь трапеции, изображённой на рисунке.
Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
3) Площадь круга меньше квадрата длины его диаметра.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CKD.
В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: