Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=122° и ∠ACB=47°. Найдите угол DCB. Ответ дайте в градусах.
Рассмотрим треугольник ACD.
По
теореме о сумме углов треугольника:
180°=∠CAB+∠ADC+∠ACD
180°=122°+∠ADC+∠ACD
∠ADC+∠ACD=58°
Так как AD=AC, то данный треугольник
равнобедренный.
Тогда, ∠ADC=∠ACD (по
свойству равнобедренного треугольника), получаем, что:
∠ADC=∠ACD=58°/2=29°
∠DCB=∠ACB-∠ACD=47°-29°=18°
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
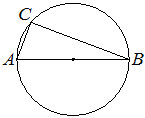Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если
угол BAC равен 74°. Ответ дайте в градусах.
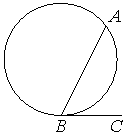На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
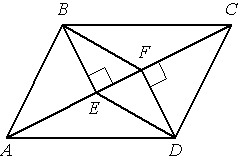В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: