Сторона AC треугольника ABC проходит через центр окружности. Найдите ∠C, если ∠A=30°. Ответ дайте в градусах.
Так как AC проходит через центр окружности, значит это диаметр.
Треугольник ABC вписан в окружность и центр окружности лежит на середине AC, следовательно треугольник ABC
прямоугольный с гипотенузой AC(по
теореме об описанной окружности).
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=30°+90°+∠C
∠C=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=7 и HD=24. Диагональ параллелограмма BD равна 51. Найдите площадь параллелограмма.
Синус острого угла A треугольника ABC равен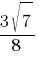 
. Найдите CosA.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=17, AC=51, NC=32.
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-26 21:48:02) Алина: Потому что ∠ABC прямоугольный =90°
(2014-05-26 18:48:07) мариша: Откуда взяли 90°?
(2014-05-19 13:03:26) ольга: можно еще через дуги. дуга bc=60 т.к. ac диаметр ,то 360:2=180 значит дуга ab=120 и т.к. <с=1/2 дуги ab, то <с=60
(2014-05-18 12:58:49) Ирина: все понятно спасибо