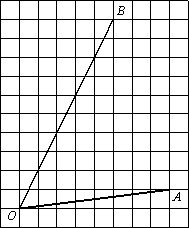
Найдите тангенс угла AOB.
Вариант №1 (Прислал пользователь Евгений)
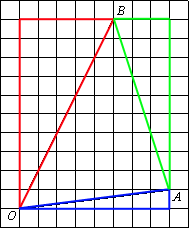Проведем отрезок AB.
Найдем каждую сторону треугольника ABO по
теореме Пифагора:
AO2=82+12
AO2=64+1=65
AO=√
AB2=92+32
AB2=81+9=90
AB=√
BO2=102+52
BO2=100+25=125
BO=√
По
теореме косинусов:
AB2=AO2+BO2-2AO*BO*cos∠AOB
(√
90=65+125-2√
-100=-2√
50=5√
10=√
10=5√
2=√
cos∠AOB=2/√
По основной тригонометрической формуле:
sin2∠AOB+cos2∠AOB=1
sin2∠AOB+(2/√
sin2∠AOB+4/13=1
sin2∠AOB=1-4/13
sin2∠AOB=13/13-4/13
sin2∠AOB=(13-4)/13
sin2∠AOB=9/13
sin∠AOB=3/√
tg∠AOB=sin∠AOB/cos∠AOB=(3/√
Ответ: tg∠AOB=1,5
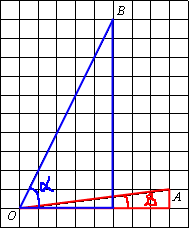Достроим чертеж до двух
прямоугольных треугольников. Найдем
тангенсы для обоих треугольников для их углов О.Поделитесь решением
Присоединяйтесь к нам...
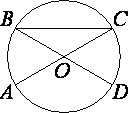В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 5 м. Найдите длину троса.
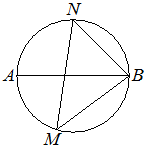На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-26 17:23:49) 2 вариант это: Аналитическая геометрия уже
(2015-02-25 14:27:47) Администратор: Светлана, интересный подход, присылайте на zapros@otvet-gotov.ru. Обязательно изучу и опубликую Ваш вариант.
(2015-02-25 13:47:48) Светлана: Можно найти через скалярное произведение векторов ОА(8;1) и ОВ(5;10),если поместить т.О в начало координат .На какой адрес можно присылать свои варианты решения?
(2015-01-19 00:12:30) Администратор: Раиса, изначально, второй вариант был единственным, но мне писали, что эта формула девятиклассникам неизвестна. Один из пользователей прислал другой вариант. Он длиннее, но зато основан на известных в девятом классе теоремах, поэтому я посчитал, что нужно показать оба варианта.
(2015-01-18 10:48:07) Раиса: Спасибо, второй вариант проще, главное, чтобы знали учащиеся формулу тангенс разности 2-х углов