Какие из следующих утверждений верны?
1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
2) Площадь трапеции равна произведению основания трапеции на высоту.
3) Треугольника со сторонами 1, 2, 4 не существует.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Рассмотрим каждое утверждение:
1) "Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу", это утверждение верно, по
определению.
2) "Площадь трапеции равна произведению основания трапеции на высоту", данное утверждение не верно, так как площадь
трапеции равна произведению полусуммы оснований на высоту.
3) "Треугольника со сторонами 1, 2, 4 не существует", это утверждение верно, т.к. длина одной из сторон не может быть больше суммы длин двух других сторон (а 4>1+2).
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
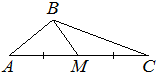В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
Сторона квадрата равна 4√2. Найдите радиус окружности, описанной около этого квадрата.
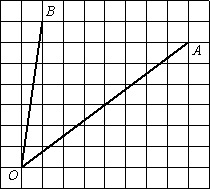Найдите тангенс угла AOB.
В треугольнике ABC известно, что ∠BAC=62°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его медианой.
2) Диагонали прямоугольника равны.
3) У любой трапеции боковые стороны равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: