Катеты прямоугольного треугольника равны 3√
Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
AB2=BC2+AC2
AB2=212+(3√
AB2=441+9*51=441+459=900
AB=30
Меньший угол лежит напротив меньшей стороны, поэтому сравним числа 21 и 3√
212 и (3√
441 и 459, очевидно, что 441<459.
Следовательно 21<3√
Синус меньшего угла будет равен
отношению меньшей стороны к гипотенузе, т.е. 21/30=0,7
Ответ: 0,7
Поделитесь решением
Присоединяйтесь к нам...
ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
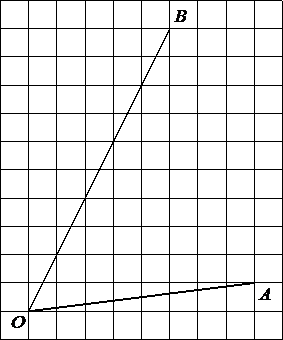Найдите тангенс угла AOB.
На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: