В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
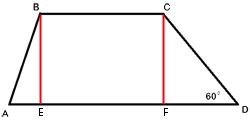Проведем
высоты BE и CF как показано на рисунке.
Рассмотрим треугольник CDF. Он
прямоугольный, т.к. CF-высота.
По
теореме о сумме углов треугольника /FCD=180°-90°-60°=30°.
По
определению синуса sin/FCD=DF/CD=sin30°=1/2
Т.е. DF=CD/2, CD, в свою очередь, по условию задачи равно AD/2, получам, что DF=AD/4.
BC=AD/2 (по условию задачи)
EF=BC=AD/2 (т.к. BCFE - прямоугольник)
Вычислим AE, AE=AD-DF-EF=AD-AD/4-AD/2=AD/4, т.е. мы получили, что AE=FD
Рассмотрим треугольники ABC и DCF:
BE=CF (т.к. BCFE - прямоугольник)
AE=FD (только что получили)
/AEF=90°=/DFC, тогда по
первому признаку равенства, треугольники ABC и DCF равны.
Следовательно, AB=CD, т.е. наша
трапеция равнобедренная.
AB=CD=4 (по условию задачи), AD=2*CD=2*BC=8 (тоже по условию), BC=CD=4
FD=AD/4=2
По
теореме Пифагора CD2=CF2+FD2
42=CF2+22
CF2=12, CF=√
CF=2√
SABCD=((BC+AD)/2)*CF=((4+8)/2)*2√
SABCD=12√
Ответ: SABCD=12√
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Если один из углов треугольника прямой, то треугольник прямоугольный.
2) Диагонали квадрата точкой пересечения делятся пополам.
3) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
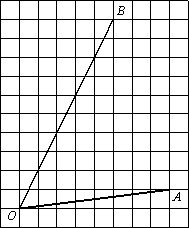Найдите тангенс угла AOB.
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина – 28 см. Найдите расстояние между точками A и B (в метрах).
Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-12-25 18:37:31) Администратор: Настя, 95, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-12-25 14:00:17) 95: Высота и отрезки на которые она делит сторону одного треугольника соответственно равны высоте и отрезкам на которые она делит сторону другого треугольника докажите что такие треугольники равны
(2016-12-25 14:00:15) 95: Высота и отрезки на которые она делит сторону одного треугольника соответственно равны высоте и отрезкам на которые она делит сторону другого треугольника докажите что такие треугольники равны
(2016-12-25 13:30:08) : Стороны треугольника пропорциональны числам 9:11:15 А разность наибольшее наименьшее сторон равна 18 см найдите периметр треугольника
(2016-12-25 13:28:28) Настя: Стороны треугольника пропали пропорциональны числам 09:11 11:15 а разность наибольшего и наименьшего сторон равна 18 см найдите периметр треугольника
(2016-12-18 17:29:20) Администратор: Настя, это первый признак равенства треугольников, доказательство данной теоремы Вы найдете в любом учебнике по геометрии.
(2016-12-18 15:03:47) Настя: BE=CF,AE=DF ,угол 1= углу 2 Доказать: треугольник ABD= треугольнику DCA