Сторона ромба равна 28, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
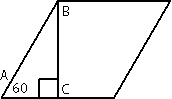Рассмотрим треугольник АВС, этот треугольник
прямоугольный (по условию задачи). /A=60°, следовательно по
теореме о сумме углов треугольника /АВС = 180°-90°-60°=30°. По
свойству прямоугольного треугольника АС=АВ/2=28/2=14. Следовательно вторая половина стороны ромба = 28-14=14. Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: длины обоих отрезков равны 14.
Поделитесь решением
Присоединяйтесь к нам...
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, описанной около этого треугольника.
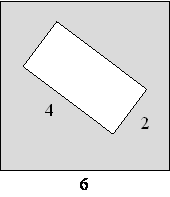Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Человек, рост которого равен 1,8 м, стоит на расстоянии 11 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).
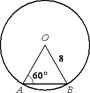Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: