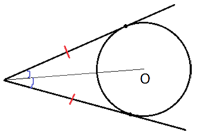
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
OK перпендикулярен к
касательной (по
свойству касательной), т.е. угол между OK и
касательной равен 90°.
Следовательно, ∠OKM=90°-7°=83°
Треугольник OMK -
равнобедренный (т.к. OM и OK - радиусы окружности и, соответственно, равны друг другу).
По
свойству равнобедренного треугольника ∠OKM=∠OMK=83°
Ответ: ∠OMK=83°
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, sinA=0,75, AC=√
Человек, рост которого равен 1,8 м, стоит на расстоянии 11 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC.
Стороны AC, AB, BC треугольника ABC равны 2√
Найдите площадь параллелограмма, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: