Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
Рассмотрим каждое утверждение.
1) "Против большей стороны треугольника лежит меньший угол", это утверждение неверно, т.к. противоречит
теореме о соотношении углов и сторон.
2) "Любой
квадрат можно вписать в
окружность", это утверждение верно, т.к. четырехугольник можно вписать в окружность, если сумма противоположных углов этого четырехугольника равна 180°.
3) "Площадь
трапеции равна произведению
средней линии на высоту", это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна
722√
Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
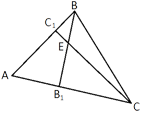Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=4:1.Прямая AK пересекает сторону BC в точке P.Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: