
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ986 –Η–Ζ 1087 |
 –£ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ―É―é ―²―Ä–Α–Ω–Β―Ü–Η―é, –Ω–Β―Ä–Η–Φ–Β―²―Ä –Κ–Ψ―²–Ψ―Ä–Ψ–Ι ―Ä–Α–≤–Β–Ϋ 180, –Α –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Α–≤–Ϋ–Α 1620, –Φ–Ψ–Ε–Ϋ–Ψ –≤–Ω–Η―¹–Α―²―¨ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ–Β–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η –¥–Ψ –Β―ë –Φ–Β–Ϋ―¨―à–Β–≥–Ψ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è.
–£ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ―É―é ―²―Ä–Α–Ω–Β―Ü–Η―é, –Ω–Β―Ä–Η–Φ–Β―²―Ä –Κ–Ψ―²–Ψ―Ä–Ψ–Ι ―Ä–Α–≤–Β–Ϋ 180, –Α –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Α–≤–Ϋ–Α 1620, –Φ–Ψ–Ε–Ϋ–Ψ –≤–Ω–Η―¹–Α―²―¨ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ–Β–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η –¥–Ψ –Β―ë –Φ–Β–Ϋ―¨―à–Β–≥–Ψ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è.
–ü–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η:
SABCD=EF*(AD+BC)/2=1620
–ü–Β―Ä–Η–Φ–Β―²―Ä ―²―Ä–Α–Ω–Β―Ü–Η–Η:
PABCD=AB+BC+CD+AD=180
AB=CD (―²–Α–Κ –Κ–Α–Κ
―²―Ä–Α–Ω–Β―Ü–Η―è ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Α―è).
–ß―²–Ψ–±―΄ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ –Φ–Ψ–Ε–Ϋ–Ψ –±―΄–Μ–Ψ –≤–Ω–Η―¹–Α―²―¨ –≤ ―²―Ä–Α–Ω–Β―Ü–Η―é –¥–Ψ–Μ–Ε–Ϋ–Ψ –≤―΄–Ω–Ψ–Μ–Ϋ―è―²―¨―¹―è ―É―¹–Μ–Ψ–≤–Η–Β - ―¹―É–Φ–Φ―΄ –Ω―Ä–Ψ―²–Η–≤–Ψ–Ω–Ψ–Μ–Ψ–Ε–Ϋ―΄―Ö ―¹―²–Ψ―Ä–Ψ–Ϋ ―²―Ä–Α–Ω–Β―Ü–Η–Η –¥–Ψ–Μ–Ε–Ϋ―΄ –±―΄―²―¨ ―Ä–Α–≤–Ϋ―΄, ―².–Β.
AD+BC=AB+CD
AD+BC=2AB (―².–Κ. AB=CD)
–Δ–Ψ–≥–¥–Α:
PABCD=AB+BC+CD+AD=AB+2AB+AB=4AB=180
AB=45
–½–Ϋ–Α―΅–Η―², AD+BC=2*45=90
SABCD=EF*(AD+BC)/2=EF*90/2=EF*45=1620
EF=36
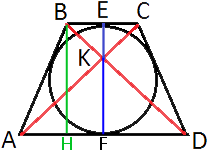 –ü―Ä–Ψ–≤–Β–¥–Β–Φ
–≤―΄―¹–Ψ―²―É BH, –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ
–≤―΄―¹–Ψ―²―É BH, –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
BH=EF=36, ―²–Α–Κ –Κ–Α–Κ BEFH -
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
AH=(AD-BC)/2
–ü–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –ü–Η―³–Α–≥–Ψ―Ä–Α:
AB2=BH2+AH2
452=362+AH2
2025=1296+AH2
729=AH2
√729=AH
27=AH=(AD-BC)/2
54=AD-BC, –≤―¹–Ω–Ψ–Φ–Ϋ–Η–Φ, ―΅―²–Ψ AD+BC=90
54=AD-(90-AD)
54=AD-90+AD
144=2AD
AD=72
–Δ–Ψ–≥–¥–Α BC=90-72=18
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η AKF –Η CKE
AF=AD/2=72/2=36
CE=BC/2=18/2=9
∠AFK=∠CEK=90¬Α
∠AKF=∠CKE (―².–Κ. –Ψ–Ϋ–Η
–≤–Β―Ä―²–Η–Κ–Α–Μ―¨–Ϋ―΄–Β)
–ü–Ψ
–Ω–Β―Ä–≤–Ψ–Φ―É –Ω―Ä–Η–Ζ–Ϋ–Α–Κ―É –Ω–Ψ–¥–Ψ–±–Η―è ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤, –¥–Α–Ϋ–Ϋ―΄–Β ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η
–Ω–Ψ–¥–Ψ–±–Ϋ―΄.
–Δ–Ψ–≥–¥–Α, AF/CE=KF/KE
36/9=KF/KE
4=(EF-KE)/KE (–≤―¹–Ω–Ψ–Φ–Ϋ–Η–Φ, ―΅―²–Ψ EF=36)
4KE=36-KE
5KE=36
KE=7,2
–û―²–≤–Β―²: 7,2
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –ü―Ä–Ψ–Β–Κ―²–Ψ―Ä –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â–Α–Β―² ―ç–Κ―Ä–Α–Ϋ A –≤―΄―¹–Ψ―²–Ψ–Ι 190 ―¹–Φ, ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι
–Ϋ–Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η 210 ―¹–Φ –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α. –ù–Α–Ι–¥–Η―²–Β, –Ϋ–Α –Κ–Α–Κ–Ψ–Φ –Ϋ–Α–Η–Φ–Β–Ϋ―¨―à–Β–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ϋ―É–Ε–Ϋ–Ψ ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Η―²―¨ ―ç–Κ―Ä–Α–Ϋ B –≤―΄―¹–Ψ―²–Ψ–Ι 380 ―¹–Φ, ―΅―²–Ψ–±―΄ –Ψ–Ϋ –±―΄–Μ –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â―ë–Ϋ, –Β―¹–Μ–Η –Ϋ–Α―¹―²―Ä–Ψ–Ι–Κ–Η –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ψ―¹―²–Α―é―²―¹―è –Ϋ–Β–Η–Ζ–Φ–Β–Ϋ–Ϋ―΄–Φ–Η. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö.
–ü―Ä–Ψ–Β–Κ―²–Ψ―Ä –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â–Α–Β―² ―ç–Κ―Ä–Α–Ϋ A –≤―΄―¹–Ψ―²–Ψ–Ι 190 ―¹–Φ, ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι
–Ϋ–Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η 210 ―¹–Φ –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α. –ù–Α–Ι–¥–Η―²–Β, –Ϋ–Α –Κ–Α–Κ–Ψ–Φ –Ϋ–Α–Η–Φ–Β–Ϋ―¨―à–Β–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ϋ―É–Ε–Ϋ–Ψ ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Η―²―¨ ―ç–Κ―Ä–Α–Ϋ B –≤―΄―¹–Ψ―²–Ψ–Ι 380 ―¹–Φ, ―΅―²–Ψ–±―΄ –Ψ–Ϋ –±―΄–Μ –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â―ë–Ϋ, –Β―¹–Μ–Η –Ϋ–Α―¹―²―Ä–Ψ–Ι–Κ–Η –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ψ―¹―²–Α―é―²―¹―è –Ϋ–Β–Η–Ζ–Φ–Β–Ϋ–Ϋ―΄–Φ–Η. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö.
 –£–Β―Ä―à–Η–Ϋ―΄ ―Ä–Ψ–Φ–±–Α ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ―΄ –Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Α―Ö –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, –Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―Ä–Ψ–Φ–±–Α –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄ –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―è–Φ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Β–Ι ―Ä–Ψ–Φ–±–Α –Η –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, –Β―¹–Μ–Η –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ–Β–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ―Ä–Α–≤–Ϋ–Ψ 28.
–£–Β―Ä―à–Η–Ϋ―΄ ―Ä–Ψ–Φ–±–Α ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ―΄ –Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Α―Ö –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, –Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ ―Ä–Ψ–Φ–±–Α –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄ –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―è–Φ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Β–Ι ―Ä–Ψ–Φ–±–Α –Η –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α, –Β―¹–Μ–Η –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ–Β–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ―Ä–Α–≤–Ϋ–Ψ 28.
 –î–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –Ψ–±―Ä–Α–Ζ―É–Β―² ―É–≥–Ψ–Μ 50¬Α ―¹ –Ψ–¥–Ϋ–Ψ–Ι –Η–Ζ –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―è–Φ–Η ―ç―²–Ψ–≥–Ψ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–î–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –Ψ–±―Ä–Α–Ζ―É–Β―² ―É–≥–Ψ–Μ 50¬Α ―¹ –Ψ–¥–Ϋ–Ψ–Ι –Η–Ζ –Β–≥–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―è–Φ–Η ―ç―²–Ψ–≥–Ψ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –Π–Β–Ϋ―²―Ä–Α–Μ―¨–Ϋ―΄–Ι ―É–≥–Ψ–Μ AOB –Ψ–Ω–Η―Ä–Α–Β―²―¹―è –Ϋ–Α ―Ö–Ψ―Ä–¥―É –ê–£ ―²–Α–Κ, ―΅―²–Ψ ―É–≥–Ψ–Μ –û–ê–£ ―Ä–Α–≤–Β–Ϋ 60¬Α. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É ―Ö–Ψ―Ä–¥―΄ –ê–£, –Β―¹–Μ–Η ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 7.
–Π–Β–Ϋ―²―Ä–Α–Μ―¨–Ϋ―΄–Ι ―É–≥–Ψ–Μ AOB –Ψ–Ω–Η―Ä–Α–Β―²―¹―è –Ϋ–Α ―Ö–Ψ―Ä–¥―É –ê–£ ―²–Α–Κ, ―΅―²–Ψ ―É–≥–Ψ–Μ –û–ê–£ ―Ä–Α–≤–Β–Ϋ 60¬Α. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É ―Ö–Ψ―Ä–¥―΄ –ê–£, –Β―¹–Μ–Η ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 7.
 –£ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–Η–Α–Φ–Β―²―Ä―΄ AD –Η BC, ―É–≥–Ψ–Μ
OCD ―Ä–Α–≤–Β–Ϋ 80¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α OAB.
–£ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–Η–Α–Φ–Β―²―Ä―΄ AD –Η BC, ―É–≥–Ψ–Μ
OCD ―Ä–Α–≤–Β–Ϋ 80¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α OAB.

–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: