
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ443 –Є–Ј 1087 |
 –С–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–Њ–≤ A –Є B –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є BC=2, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є K –і–Њ —Б—В–Њ—А–Њ–љ—Л AB —А–∞–≤–љ–Њ 1.
–С–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–Њ–≤ A –Є B –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є BC=2, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є K –і–Њ —Б—В–Њ—А–Њ–љ—Л AB —А–∞–≤–љ–Њ 1.
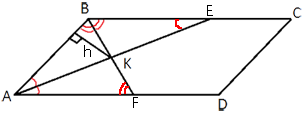 –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П
–±–Є—Б—Б–µ–Ї—В—А–Є—Б —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П
–±–Є—Б—Б–µ–Ї—В—А–Є—Б —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
∠FAK=∠BEK (—В.–Ї. —Н—В–Њ
–љ–∞–Ї—А–µ—Б—В-–ї–µ–ґ–∞—Й–Є–µ —Г–≥–ї—Л).
–Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ ∠BAK=∠BEK, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABE -
—А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є (–њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞).
–Ґ–Њ–≥–і–∞ AB=BE.
–Ґ—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABK –Є EBK —А–∞–≤–љ—Л –њ–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г —А–∞–≤–µ–љ—Б—В–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –Є
–≤—Л—Б–Њ—В—Л —Г —Н—В–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ —В–Њ–ґ–µ —А–∞–≤–љ—Л.
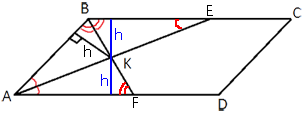 –Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ, —А–∞–≤–љ—Л –Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABK –Є AFK.
–Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ, —А–∞–≤–љ—Л –Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABK –Є AFK.
–Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ –≤—Л—Б–Њ—В–∞
–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ —А–∞–≤–љ–∞ 2h.
–Я–ї–Њ—Й–∞–і—М
–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ —А–∞–≤–љ–∞ SABCD=2h*BC=2*1*2=4
–Ю—В–≤–µ—В: SABCD=4
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є AB=19 –Є CD=28 –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –њ—А–Є—З—С–Љ ∠
AKB=60¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є AB=19 –Є CD=28 –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –њ—А–Є—З—С–Љ ∠
AKB=60¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
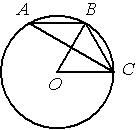 –Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /BOC=60¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BAC (–≤ –≥—А–∞–і—Г—Б–∞—Е).
–Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /BOC=60¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BAC (–≤ –≥—А–∞–і—Г—Б–∞—Е).
–£–Ї–∞–ґ–Є—В–µ –љ–Њ–Љ–µ—А–∞ –≤–µ—А–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є.
1) –Х—Б–ї–Є –Њ–і–Є–љ –Є–Ј —Г–≥–ї–Њ–≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –њ—А—П–Љ–Њ–є, —В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є.
2) –Ф–Є–∞–≥–Њ–љ–∞–ї–Є –Ї–≤–∞–і—А–∞—В–∞ —В–Њ—З–Ї–Њ–є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–µ–ї—П—В—Б—П –њ–Њ–њ–Њ–ї–∞–Љ.
3) –Ґ–Њ—З–Ї–∞, —А–∞–≤–љ–Њ—Г–і–∞–ї—С–љ–љ–∞—П –Њ—В –Ї–Њ–љ—Ж–Њ–≤ –Њ—В—А–µ–Ј–Ї–∞, –ї–µ–ґ–Є—В –љ–∞ —Б–µ—А–µ–і–Є–љ–љ–Њ–Љ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–µ –Ї —Н—В–Њ–Љ—Г –Њ—В—А–µ–Ј–Ї—Г.
 –Э–∞ —А–Є—Б—Г–љ–Ї–µ –Є–Ј–Њ–±—А–∞–ґ—С–љ –Ї–Њ–ї–Њ–і–µ—Ж —Б ¬Ђ–ґ—Г—А–∞–≤–ї—С–Љ¬ї. –Ъ–Њ—А–Њ—В–Ї–Њ–µ –њ–ї–µ—З–Њ –Є–Љ–µ–µ—В –і–ї–Є–љ—Г 2 –Љ, –∞ –і–ї–Є–љ–љ–Њ–µ –њ–ї–µ—З–Њ вАФ 6 –Љ. –Э–∞ —Б–Ї–Њ–ї—М–Ї–Њ –Љ–µ—В—А–Њ–≤ –Њ–њ—Г—Б—В–Є—В—Б—П –Ї–Њ–љ–µ—Ж –і–ї–Є–љ–љ–Њ–≥–Њ –њ–ї–µ—З–∞, –Ї–Њ–≥–і–∞ –Ї–Њ–љ–µ—Ж –Ї–Њ—А–Њ—В–Ї–Њ–≥–Њ –њ–Њ–і–љ–Є–Љ–µ—В—Б—П –љ–∞ 1,5 –Љ?
–Э–∞ —А–Є—Б—Г–љ–Ї–µ –Є–Ј–Њ–±—А–∞–ґ—С–љ –Ї–Њ–ї–Њ–і–µ—Ж —Б ¬Ђ–ґ—Г—А–∞–≤–ї—С–Љ¬ї. –Ъ–Њ—А–Њ—В–Ї–Њ–µ –њ–ї–µ—З–Њ –Є–Љ–µ–µ—В –і–ї–Є–љ—Г 2 –Љ, –∞ –і–ї–Є–љ–љ–Њ–µ –њ–ї–µ—З–Њ вАФ 6 –Љ. –Э–∞ —Б–Ї–Њ–ї—М–Ї–Њ –Љ–µ—В—А–Њ–≤ –Њ–њ—Г—Б—В–Є—В—Б—П –Ї–Њ–љ–µ—Ж –і–ї–Є–љ–љ–Њ–≥–Њ –њ–ї–µ—З–∞, –Ї–Њ–≥–і–∞ –Ї–Њ–љ–µ—Ж –Ї–Њ—А–Њ—В–Ї–Њ–≥–Њ –њ–Њ–і–љ–Є–Љ–µ—В—Б—П –љ–∞ 1,5 –Љ?
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 150¬∞, AB=4. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 150¬∞, AB=4. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2018-01-19 20:25:44) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ф–∞—А–Є–љ–∞, —В–∞–Ї –Ї–∞–Ї —Н—В–Њ –≤—Л—Б–Њ—В—Л —А–∞–≤–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ ABK –Є EBK.
(2018-01-03 15:39:26) –і–∞—А–Є–љ–∞: –Я–Њ—З–µ–Љ—Г –≤—Л—Б–Њ—В—Л —А–∞–≤–љ—Л?
(2017-02-20 20:19:01) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Р—А—В–µ–Љ, –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ —А–∞–≤–љ–∞ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—О –≤—Л—Б–Њ—В—Л –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ –Є —Б—В–Њ—А–Њ–љ—Л –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞. –Т —Н—В–Њ–є –Ј–∞–і–∞—З–µ –≤—Л—Б–Њ—В–∞ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ –њ–Њ–ї—Г—З–Є–ї–∞—Б—М —А–∞–≤–љ–∞ –і–≤—Г–Љ –≤—Л—Б–Њ—В–∞–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ (–љ–∞—З–µ—А—З–µ–љ—Л —Б–Є–љ–Є–Љ —Ж–≤–µ—В–Њ–Љ), –њ–Њ—Н—В–Њ–Љ—Г S=2h*BC (h=1, BC=2) => S=2*1*2=4
(2017-02-20 15:53:39) –Р—А—В–µ–Љ: –Я–Њ—З–µ–Љ—Г 2h, –∞ –љ–µ 3? –Ґ–∞–Љ –ґ–µ —Г —В—А—С—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Њ–≤ –≤—Л—Б–Њ—В—Л.
(2017-02-20 15:48:02) –Р—А—В–µ–Љ: –Ч–∞—З–µ–Љ –≤—Л –µ—Й—С –љ–∞ 1 –і–Њ–Љ–љ–Њ–ґ–∞–ї–Є? –Я–Њ —Д–Њ—А–Љ—Г–ї–µ –љ–∞–і–Њ h*–љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ.