
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ529 –Є–Ј 1087 |
–Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 392√
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ:
a - –Є—Б–Ї–Њ–Љ—Л–є –Ї–∞—В–µ—В
b - –≤—В–Њ—А–Њ–є –Ї–∞—В–µ—В
c - –≥–Є–њ–Њ—В–µ–љ—Г–Ј–∞
sin30°=1/2 (
—В–∞–±–ї–Є—З–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ)
sin30¬∞=a/c=1/2 (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О —Б–Є–љ—Г—Б–∞)
c=2a
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
a2+b2=c2
a2+b2=(2a)2
b2=3a2
b=a√
–Ш–Ј —Г—Б–ї–Њ–≤–Є—П: S—В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞=ab/2=392√
a*a√
–°–Њ–Ї—А–∞—Й–∞–µ–Љ √
a2=392*2=784
a=28
–Ю—В–≤–µ—В: a=28
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–Є–∞–≥–Њ–љ–∞–ї–µ–є —А–Њ–Љ–±–∞ –і–Њ –Њ–і–љ–Њ–є –Є–Ј –µ–≥–Њ —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–Њ 19, –∞ –Њ–і–љ–∞ –Є–Ј –і–Є–∞–≥–Њ–љ–∞–ї–µ–є —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 76. –Э–∞–є–і–Є—В–µ —Г–≥–ї—Л —А–Њ–Љ–±–∞.
–†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–Є–∞–≥–Њ–љ–∞–ї–µ–є —А–Њ–Љ–±–∞ –і–Њ –Њ–і–љ–Њ–є –Є–Ј –µ–≥–Њ —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–Њ 19, –∞ –Њ–і–љ–∞ –Є–Ј –і–Є–∞–≥–Њ–љ–∞–ї–µ–є —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 76. –Э–∞–є–і–Є—В–µ —Г–≥–ї—Л —А–Њ–Љ–±–∞.
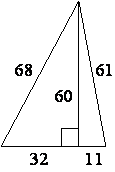 –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–≥–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–≥–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
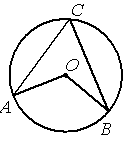 –Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /ACB=62¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ AOB (–≤ –≥—А–∞–і—Г—Б–∞—Е).
–Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /ACB=62¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ AOB (–≤ –≥—А–∞–і—Г—Б–∞—Е).
 –Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ NPQM –і–Є–∞–≥–Њ–љ–∞–ї—М NQ —П–≤–ї—П–µ—В—Б—П –±–Є—Б—Б–µ–Ї—В—А–Є—Б–Њ–є —Г–≥–ї–∞ PNM –Є –њ–µ—А–µ—Б–µ–Ї–∞–µ—В—Б—П —Б –і–Є–∞–≥–Њ–љ–∞–ї—М—О PM –≤ —В–Њ—З–Ї–µ S. –Э–∞–є–і–Є—В–µ NS, –µ—Б–ї–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –Њ–Ї–Њ–ї–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ NPQM –Љ–Њ–ґ–љ–Њ –Њ–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, PQ=86, SQ=43.
–Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ NPQM –і–Є–∞–≥–Њ–љ–∞–ї—М NQ —П–≤–ї—П–µ—В—Б—П –±–Є—Б—Б–µ–Ї—В—А–Є—Б–Њ–є —Г–≥–ї–∞ PNM –Є –њ–µ—А–µ—Б–µ–Ї–∞–µ—В—Б—П —Б –і–Є–∞–≥–Њ–љ–∞–ї—М—О PM –≤ —В–Њ—З–Ї–µ S. –Э–∞–є–і–Є—В–µ NS, –µ—Б–ї–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –Њ–Ї–Њ–ї–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ NPQM –Љ–Њ–ґ–љ–Њ –Њ–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, PQ=86, SQ=43.
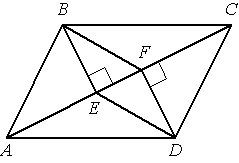 –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ –Р–Т–°D –њ—А–Њ–≤–µ–і–µ–љ—Л –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А—Л –Т–Х –Є DF –Ї –і–Є–∞–≥–Њ–љ–∞–ї–Є –Р–° (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є BEF –Є DFE —А–∞–≤–љ—Л.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ –Р–Т–°D –њ—А–Њ–≤–µ–і–µ–љ—Л –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А—Л –Т–Х –Є DF –Ї –і–Є–∞–≥–Њ–љ–∞–ї–Є –Р–° (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є BEF –Є DFE —А–∞–≤–љ—Л.
| α | sinα | cosα | tgα | ctgα |
| 0° | 0 | 1 | 0 | --- |
| 30° | 1/2 | à |
√ |
√ |
| 45° | à |
√ |
1 | 1 |
| 60° | à |
1/2 | √ |
√ |
| 90° | 1 | 0 | --- | 0 |
| 120° | à |
-1/2 | -√ |
0 |
| 135° | à |
-√ |
-1 | -1 |
| 150° | 1/2 | -à |
-√ |
-√ |
| 180° | 0 | -1 | 0 | --- |
| 210° | -1/2 | -à |
√ |
√ |
| 225° | -à |
-√ |
1 | 1 |
| 240° | -à |
-1/2 | √ |
√ |
| 270° | -1 | 0 | --- | 0 |
| 300° | -à |
1/2 | -√ |
-√ |
| 315° | -à |
√ |
-1 | -1 |
| 330° | -1/2 | à |
-√ |
-√ |
| 360° | 1 | 0 | 0 | --- |
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: