
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ682 –Є–Ј 1087 |
 –Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 882√
–Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 882√
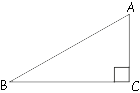 –Я–ї–Њ—Й–∞–і—М
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ –њ–Њ–ї–Њ–≤–Є–љ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –Ї–∞—В–µ—В–Њ–≤:
–Я–ї–Њ—Й–∞–і—М
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ –њ–Њ–ї–Њ–≤–Є–љ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –Ї–∞—В–µ—В–Њ–≤:
S=AC*BC/2=882√
–Я—Г—Б—В—М 60-–Є –≥—А–∞–і—Г—Б–∞–Љ —А–∞–≤–µ–љ —Г–≥–Њ–ї BAC.
–Ґ–∞–љ–≥–µ–љ—Б BAC:
td∠BAC=tg60¬∞=BC/AC=√
BC=AC√
S=AC*BC/2=AC*(AC√
AC2√
AC2/2=882
AC2=1764
AC=42
–Ю—В–≤–µ—В: 42
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ 60¬∞, –∞ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 8.
–Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ 60¬∞, –∞ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 8.
 –Я—А—П–Љ–∞—П, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞—П —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є BC –≤ —В–Њ—З–Ї–∞—Е K –Є M —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Э–∞–є–і–Є—В–µ AC, –µ—Б–ї–Є BK:KA=1:2, KM=23.
–Я—А—П–Љ–∞—П, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞—П —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є BC –≤ —В–Њ—З–Ї–∞—Е K –Є M —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Э–∞–є–і–Є—В–µ AC, –µ—Б–ї–Є BK:KA=1:2, KM=23.
 –°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 8, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —Ж–µ–љ—В—А–∞ —А–Њ–Љ–±–∞ –і–Њ –љ–µ—С —А–∞–≤–љ–Њ 2. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —А–Њ–Љ–±–∞.
–°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 8, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —Ж–µ–љ—В—А–∞ —А–Њ–Љ–±–∞ –і–Њ –љ–µ—С —А–∞–≤–љ–Њ 2. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —А–Њ–Љ–±–∞.
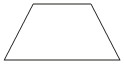 –Ю–і–Є–љ –Є–Ј —Г–≥–ї–Њ–≤ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–µ–љ 113¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ю–і–Є–љ –Є–Ј —Г–≥–ї–Њ–≤ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–µ–љ 113¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –С–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–Њ–≤ A –Є B –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є BC=11, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є K –і–Њ —Б—В–Њ—А–Њ–љ—Л AB —А–∞–≤–љ–Њ 3.
–С–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–Њ–≤ A –Є B –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є BC=11, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є K –і–Њ —Б—В–Њ—А–Њ–љ—Л AB —А–∞–≤–љ–Њ 3.





–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2017-10-04 18:09:01) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Э–Є–≥–µ—А228, –Ї–≤–∞–і—А–∞—В–љ—Л–є –Ї–Њ—А–µ–љ—М –Є–Ј 1764 –Є –µ—Б—В—М 42.
(2017-10-03 22:00:15) –Э–Є–≥–µ—А228: –Ъ–∞–Ї –Љ—Л –Є–Ј 1764 –њ–Њ–ї—Г—З–Є–ї–Є 42?
(2017-02-24 20:00:00) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ь–∞—И–∞, —З–µ—А–µ–Ј —В–∞–љ–≥–µ–љ—Б –ї–µ–≥—З–µ —А–µ—И–∞—В—М, –њ–Њ—В–Њ–Љ—Г, —З—В–Њ –Є —В–∞–љ–≥–µ–љ—Б –Є –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –≤—Л—А–∞–ґ–∞—О—В—Б—П —З–µ—А–µ–Ј –Ї–∞—В–µ—В—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞. –Х—Б–ї–Є —А–µ—И–∞—В—М —З–µ—А–µ–Ј –Ї–Њ—Б–Є–љ—Г—Б –Є–ї–Є —Б–Є–љ—Г—Б, —В–Њ –њ—А–Є–і–µ—В—Б—П –≤–≤–Њ–і–Є—В—М –µ—Й–µ –Њ–і–љ—Г –љ–µ–Є–Ј–≤–µ—Б—В–љ—Г—О - –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Г, –∞ —Н—В–Њ —Б–Є–ї—М–љ–Њ —Г—Б–ї–Њ–ґ–љ–Є—В —А–µ—И–µ–љ–Є–µ.
(2017-02-24 18:30:27) –Љ–∞—И–∞: –њ–Њ—З–µ–Љ—Г –љ–∞–і–Њ –Є—Б–Ї–∞—В—М —В–∞–љ–≥–µ–љ—Б –∞ –љ–µ –Ї–Њ—Б–Є–љ—Г—Б –Є–ї–Є —Б–Є–љ—Г—Б?