
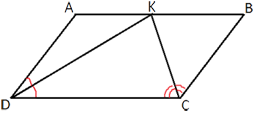 Биссектрисы углов C и D параллелограмма ABCD пересекаются в точке K стороны AB. Докажите, что K — середина AB.
Биссектрисы углов C и D параллелограмма ABCD пересекаются в точке K стороны AB. Докажите, что K — середина AB.
∠CDK=∠AKD (т.к. это
накрест-лежащие углы).
Так как DK -
биссектриса, то:
∠CDK=∠ADK.
Получается, что треугольник AKD -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда, по
определению равнобедренного треугольника:
AD=AK.
∠DCK=∠CKB (т.к. это
накрест-лежащие углы).
Так как CK -
биссектриса, то:
∠DCK=∠KCB.
Получается, что треугольник CKB -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда, по
определению равнобедренного треугольника:
BC=BK.
AD=BC (по
свойству
параллелограмма), следовательно:
AK=KB
Поделитесь решением
Присоединяйтесь к нам...
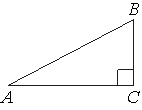 В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
 Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
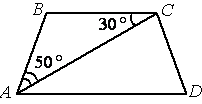 Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
Комментарии:
(2018-02-25 20:24:08) Администратор: da13, не за что)
(2018-02-25 20:18:43) da13: Я поняла) СПасибо!
(2018-02-25 20:16:38) da13: Почему СК - биссектриса?
(2016-09-22 15:59:07) Администратор: Карина, мы не помогаем делать домашнее задание, а разбираем задачи, которые будут на экзаменах. Эти задачи берутся с сайта fipi.ru.
(2016-09-22 15:30:19) карина: ав=сд ас=ад доказать что параллелограмм