
 Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
 Площадь любого треугольника равна половине произведения
высоты и стороны, к которой
высота проведена.
Площадь любого треугольника равна половине произведения
высоты и стороны, к которой
высота проведена.
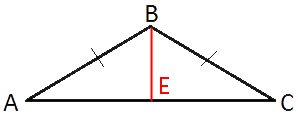
Проведем
высоту как показано на рисунке.
По
свойству равнобедренного треугольника BE - и
высота, и
медиана. Следовательно, AE=EC=AC/2.
Треугольник ABE -
прямоугольный (т.к. BE -
высота).
По
теореме Пифагора найдем высоту BE:
AB2=AE2+BE2
AB2=(AC/2)2+BE2
342=(60/2)2+BE2
1156=900+BE2
BE2=256
BE=16
SABC=(BE*AC)/2=(16*60)/2=16*30=480
Ответ: SABC=480
Поделитесь решением
Присоединяйтесь к нам...
Синус острого угла A треугольника ABC равен 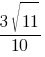 . Найдите CosA.
. Найдите CosA.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
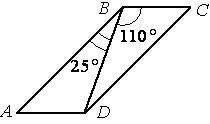 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
 Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Комментарии:
(2014-05-28 22:37:16) Администратор: Павел, правильно заданный вопрос - это половина правильного ответа )))
(2014-05-28 21:36:02) Павел: Только написал и сразу понял
(2014-05-28 21:35:07) Павел: Откуда в 4 строчке 900?