
 Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Вариант №1
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=∠A+65°+85°
∠A=180°-65°-85°=30°
По
теореме синусов:
2R=BC/sin∠A
2R=BC/sin30°=BC/(1/2)=2BC
R=BC=14
Ответ: 14
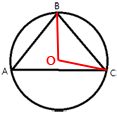 Проведем два отрезка из центра к точкам B и C, как показано на рисунке.
Проведем два отрезка из центра к точкам B и C, как показано на рисунке.Поделитесь решением
Присоединяйтесь к нам...
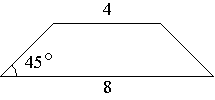 В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
 В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
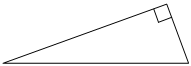 В прямоугольном треугольнике катет и гипотенуза равны 7 и 25 соответственно. Найдите другой катет этого треугольника.
В прямоугольном треугольнике катет и гипотенуза равны 7 и 25 соответственно. Найдите другой катет этого треугольника.
 Катеты прямоугольного треугольника равны √
Катеты прямоугольного треугольника равны √
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Комментарии:
(2020-05-15 22:14:28) Администратор: Татьяна, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2020-05-08 17:19:06) татьяна: Точка О - центр кола, АВ - його хорда. Знайдіть кут АОВ, якщо кут ОАВ дорівнює 65°
(2017-04-30 23:00:08) Администратор: Надежда, мне понравилось Ваше решение, поэтому я его опубликовал. Правда, из-за объяснений оно получилось длиннее, но как мне кажется, проще, поэтому должно быть понятней. Спасибо за предложенный вариант.
(2017-04-29 23:41:07) Надежда: Можно решить проще.Через вписанный и центральный угол ВОС=60.
(2017-03-17 02:11:35) Администратор: Роман, напишите, пожалуйста, свой вариант решения. Если он будет проще, то я его опубликую под Вашим именем.
(2017-03-16 18:48:20) Роман: Сложно. Все гораздо проще. Внимательно нужно посмотреть на чертеж и треугольник ВСО, где О центр окружности.
(2017-02-26 21:19:01) Администратор: Кс, попрошу без оскарблений. Раз так много недопониманий, поясняю популярно.
1. По теореме \"против угла в 30 градусов лежит катет равный половине гипотенузы\" - это работает только для прямоугольного треугольника (в обычном треугольнике нет ни катетов ни гипотенузы). В нашем треугольнике ни один из углов не равен 90 градусам. Поэтому все остальное решение неверно и только случайно привело к верному ответу.
2. Фраза \" через радиусы и сторону правильных многоугольников описанных окр-ть нельзя\" мне вообще непонятна, что-то с падежами.
3. Я так и не получил ответ на свой вопрос \"что в условии дано лишнего или не использованного при решении?\".
4. Я могу предложить еще несколько решений, но, поверьте, легче они не будут.
(2017-02-26 21:03:00) Кс: Администратор вы туп( и нечего сказать! Некоторые люди просто говорят как проще, а вы несёте чушь...
(2017-02-24 19:09:17) Администратор: Екатерина, я не понял, что Вам не нравится в решении? И что в условии дано лишнего или не использованного при решении?
(2017-02-24 17:15:06) Екатерина: Её конечно проще решить через теорему сисусон,но в задачах ОГЭ второй части никогда не дают лишнего, так что надо её решить по-другому, через радиусы и сторону правильных многоугольников описанных окр-ть нельзя, у меня нет других вариантов.
(2016-01-08 18:21:55) Администратор: Башковитый Владимир, а откуда Вы взяли, что AC=Два радиуса? В условии этого нет.
(2016-01-06 19:40:06) Башковитый Владимир: По теореме "против угла в 30 градусов лежит катет равный половине гипотенузы " AC = Два радиуса , а радиус равен 14 ,значит AC = 28 , а значит BC равно 28:2=14
(2014-05-24 18:21:40) Администратор: Алина, потому что так проще решить. А что Вас не устраивает?
(2014-05-24 14:32:16) Алина : А почему вы делаете по теореме синусов?