
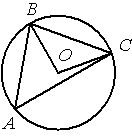
 Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=100°, этот угол является
центральным, соответственно дуга ВC (верхняя часть) тоже равна 100°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 100/2=50.
Ответ: /BAC=50°.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 37°, угол ABC равен 25°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 37°, угол ABC равен 25°. Найдите угол ACB. Ответ дайте в градусах.
 Найдите площадь квадрата, описанного около окружности радиуса 32.
Найдите площадь квадрата, описанного около окружности радиуса 32.
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
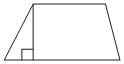 Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
 Прямые m и n параллельны. Найдите ∠3, если ∠1=22°, ∠2=72°. Ответ дайте в градусах.
Прямые m и n параллельны. Найдите ∠3, если ∠1=22°, ∠2=72°. Ответ дайте в градусах.
Комментарии: