
Дана арифметическая прогрессия: -3; 1; 5; … . Найдите сумму первых шестидесяти её членов.
Чтобы найти сумму
арифметической прогрессии у нас есть
две формулы.
a60 мы не знаем, поэтому воспользуемся второй формулой. Для этого найдем d - разность прогрессии.
d=a2-a1=1-(-3)=4.
Подставляем все в формулу:
S60=60*(2*(-3)+(60-1)*4)/2=60*(-6+236)/2=60*115=6900
Ответ: S60=6900
Поделитесь решением
Присоединяйтесь к нам...
Последовательность (bn) задана условиями: b1=4, 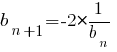
Найдите b3.
Последовательность (bn) задана условиями b1=-6, bn+1=-2*(1/bn). Найдите b5.
Геометрическая прогрессия задана условием bn=160*(3)n. Найдите сумму первых её 7 членов.
Дана арифметическая прогрессия (an), разность которой равна 2,5, a1=8,7. Найдите a9.
Записаны первые три члена арифметической прогрессии: -7; -1; 5; … Какое число стоит в этой арифметической прогрессии на 91-м месте?
Комментарии:
(2016-05-12 19:13:18) Мария: Огромное спасибо,теперь все понятно
(2015-03-06 16:08:48) Администратор: По сути, это одна и та же формула, просто для первой надо знать a1 и an, а для второй a1 и d.
(2015-03-06 13:36:44) : в чем различие двух формул?
(2015-03-03 22:03:01) Администратор: Жанна, можно и через первую формулу. Решение не обязательно одно. А запомнить надо обе формулы, пригодится...
(2015-03-03 21:57:41) Жанна: А почему нельзя найти 60-й член прогрессии, а потом сумму найти по более легкой формуле? Мне кажется это короче и легче запомнить формулу
(2015-02-20 17:50:32) Администратор: Соня, рад, что смог помочь.
(2015-02-20 17:36:32) Соня: Я поняла как найти шестидесятый член. Спасибо ):
(2014-05-19 20:49:34) Администратор: Майя, картинки формул возвращены на место (странно, что они пропали). Здесь мы используем формулу S=(2a1+(n-1)d)*n/2
(2014-05-19 20:25:16) майя: Я не поняла, в какую формулу мы подставляем?