
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и значениями их производной в точке x=1.
ГРАФИКИ
А) 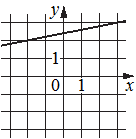 Б)
Б) 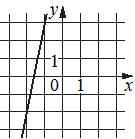 В)
В) 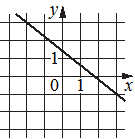 Г)
Г) 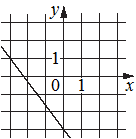
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1) 0,2
2) -4/3
3) -0,8
4) 5
В таблице под каждой буквой укажите соответствующий номер.
Про условию данной задачи сразу надо дать комментарий.
Производная от линейной функции (чем и является y=kx+b) - величина постоянная, т.е. при любом значении х производная меняться не будет, поэтому фраза "значениями их производной в точке x=1" смысла не имеет.
Скорее всего, это единое условие для целой группы задач, где будут присутствовать не только линейные функции, тогда это фраза обязательна.
Приступим к решению.
y'=(kx+b)'=k
Т.е. производная от этой функции - это коэффициент k.
Чтобы его найти, надо посмотреть на график и подставить в уравнение прямой две точки графика (т.е. значения x и y) и решить полученную систему уравнений.
Рассмотрим график А).
Лучше выбирать точку с целыми значениями x и y, тогда вычисления будут точными.
По графику А) видим, что ему принадлежат точки (-2;2) и (3;3).
Подставляем их в функцию:
Для первой точки: 2=-2k+b
Для второй точки: 3=3k+b
Это и есть система уравнений, которую надо решить любым способом и найти k - это и будет производная для первой функции.
Легче всего будет вычесть из второго уравнения первое, чтобы избавиться от b (это один из способов решения системы уранений):
3-2=3k+b-(-2k+b)
1=3k+b+2k-b
1=5k
k=1/5=0,2
Т.е. для графика А) ответ 1).
Рассмотрим график Б):
(-2;-2) и (-1;3) - точки, принадлежащие графику.
-2=-2k+b
3=-k+b
Полученная система уравнений, точно также вычтем из второго первое:
3-(-2)=-k+b-(-2k+b)
3+2=-k+b+2k-b
5=k - ответ 4)
График В).
(-2;3) и (3;-1) - точки.
3=-2k+b
-1=3k+b
Вычитаем:
-1-3=3k+b-(-2k+b)
-4=3k+b+2k-b
-4=5k
k=-4/5=-0,8 - ответ 3)
График Г).
(-3;1) и (0;-3) - точки.
1=-3k+b
-3=0*k+b => -3=b
Сейчас можно не вычитать, а просто подставить полученное значение b в первое уравнение:
1=-3k-3
3k=-3-1
3k=-4
k=-4/3 - ответ 2).
Ответ:
| График | А) | Б) | В) | Г) |
| Производная | 1) | 4) | 3) | 2) |
Поделитесь решением
Присоединяйтесь к нам...
На графике изображена зависимость частоты пульса гимнаста от времени
в течение и после его выступления в вольных упражнениях.
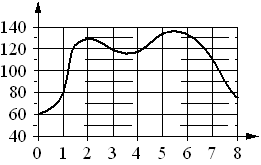
На горизонтальной оси отмечено время (в минутах), прошедшее с начала выступления гимнаста, на вертикальной оси — частота пульса (в ударах в минуту).
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику пульса гимнаста на этом интервале.
| ИНТЕРВАЛЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 4-5 мин. | 1) частота пульса упала до 110 уд./мин. |
| Б) 5-6 мин. | 2) частота пульса упала ниже 80 уд./мин. |
| В) 6-7 мин. | 3) частота пульса достигла максимума за всё время выступления и после него |
| Г) 7-8 мин. | 4) частота пульса росла на всём интервале |
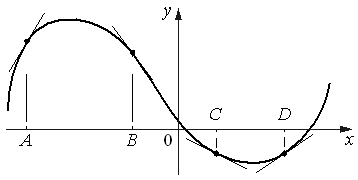 На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| A |
1) 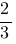
|
| B |
2) 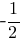
|
| C |
3) 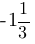
|
| D |
4) 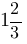
|
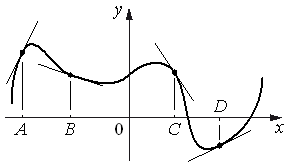 На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| A | 1) -1,5 |
| B | 2) 0,5 |
| C | 3) 2 |
| D | 4) -0,3 |
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
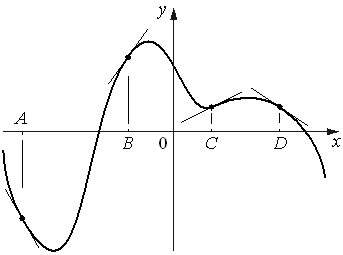
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| А | 1) -0,7 |
| B | 2) 1,4 |
| C | 3) -1,8 |
| D | 4) 0,5 |
Установите соответствие между графиками функций и характеристиками этих функций на отрезке [-1;1].
ГРАФИКИ
А) 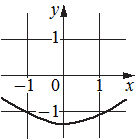 Б)
Б) 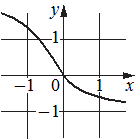 В)
В) 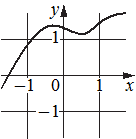 Г)
Г) 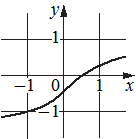
ХАРАКТЕРИСТИКИ
1) функция принимает отрицательное значение в каждой точке отрезка [-1;1]
2) функция возрастает на отрезке [-1;1]
3) функция принимает положительное значение в каждой точке отрезка [-1;1]
4) функция убывает на отрезке [-1;1]
В таблице под каждой буквой укажите соответствующий номер.
Комментарии: