Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Вариант №1 (Предложил пользователь Елена)
Проведем отрезок MP, как показано на рисунке. BM - диаметр малой окружности (по условию задачи), следовательно треугольник BMP -
прямоугольный с гипотенузой BM (по
свойству описанной окружности).
К тому же, по условию задачи, точка Р - середина стороны BC, т.е. BM -
серединный перпендикуляр к стороне BC.
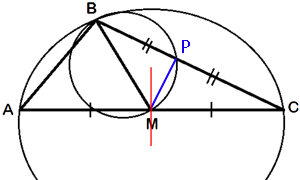Проведем
серединный перпендикуляр к стороне AC, как показано на рисунке.
Центр
описанной окружности совпадает с точкой пересечения
серединных перпендикуляров треугольника, а в данном случае - это точка М, т.е. точка М и есть центр
описанной окружности.
Так как получилось, что центр окружности лежит на стороне описываемого треугольника, то AM и MC - радиусы данной окружности и равны R=AC/2=4/2=2.
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
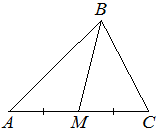В треугольнике ABC известно, что AC=14, BM — медиана, BM=10. Найдите AM.
Найдите площадь треугольника, изображённого на рисунке.
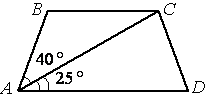Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
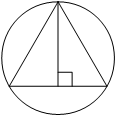Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: